This work is joint research with Jaeyong Lee.
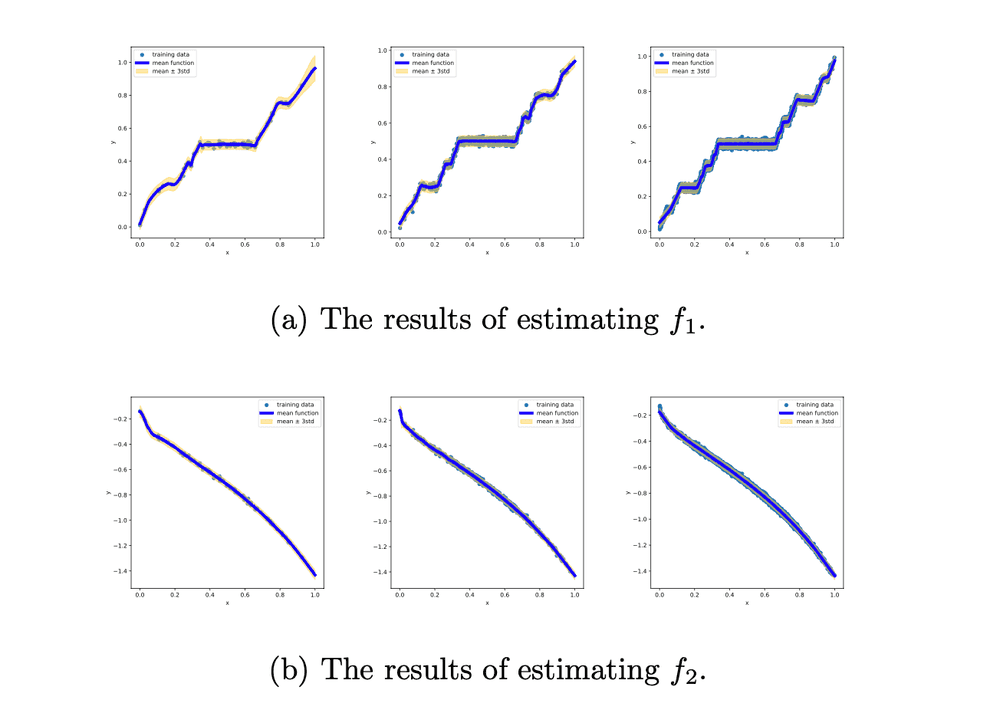
In this project, we have been studying the theoretical properties of Bayesian neural network (BNN) models and their applications. From the empirical results that neural networks have shown strong predictive power when dealing with various unstructured data such as images and natural languages, we try to figure out why and how the neural networks show these results. We showed that BNN models have optimal convergence rates in discontinuous, or non-smooth function spaces where the traditional statistical model does not work well. To verify the theoretical properties, I implemented approximated Bayesian inference of BNN models based on variational approximation and Markov chain monte carlo (MCMC) algorithms. We presented results on nonparametric regression problems at the Neural Information Processing Systems in 2022. This research is currently the topic of my PhD thesis.
Publication
*K. Lee∗, and J. Lee. (2022). Asymptotic properties for Bayesian neural network in Besov space. Advances in Neural Information Processing Systems, 35.