porgramming software R

R과 BLAS

Posted by Kyeongwon Lee on Sunday, February 6, 2022

사람들은 “R은 느리다"는 말을 자주 합니다. 저 또한 이 말에 깊이 공감하며 계산 중 병목이 발생하는 부분은 벡터화(vectorize) 연산이나 C++ 코드를 사용해 속도 향상을 꾀하고 있습니다. 그러나 여기서도 해결하지 못하는 문제가 하나 있습니다. 바로 행렬 연산입니다. 자료를 분석하다 보면 벡터, 행렬 연산을 많이 사용하게 되는데 여기서 발생하는 병목은 해결이 어려웠습니다. 그렇다면 행렬 연산에서 R의 속도 저하는 어디에서 오는 것이고, 어떻게 빠르게 할 수 있을까요?

최근 재미있는 글을 읽었습니다. R의 BLAS 라이브러리를 바꾸었을 때 계산 속도에 큰 향상이 있었다는 글이었습니다. 요지는 이렇습니다. 우리가 CRAN에서 다운로드한 R 배포판은 선형 대수학 연산을 위해 표준 BLAS/LAPACK 라이브러리를 사용합니다. 이러한 구현은 안정적이고 플랫폼 간 호환이 가능하도록 구축되었지만 성능에는 최적화되어 있지 않습니다. 바꾸어말하면 사용중인 플랫폼에 최적화된 라이브러리를 사용할 경우 속도 향상을 꾀할 수 있을 것입니다.

오늘은 이와 관련된 글을 써보려 합니다. BLAS가 무엇인지, R의 BLAS를 어떻게 바꿀 수 있는 지에 대한 이야기를 해보겠습니다.

BLAS

BLAS(Basic Linear Algebra Subprograms)는 선형 대수(linear algebra)의 연산들을 구현한 저수준 루틴(low-level routines)입니다. 구현된 연산에는 벡터의 덧셈(addition), 스칼라 곱(scalar multiplication), 내적(inner product), 선형 조합(linear combination)과 행렬 곱셈(matrix multiplication) 등이 있습니다.

BLAS의 기능은 “레벨”(level)이라는 세 가지 세트로 세분화됩니다.

  • 레벨 1 BLAS는 스칼라-벡터, 벡터-벡터 연산을 수행합니다. $$y \leftarrow \alpha x + y$$
  • 레벨 2 BLAS는 행렬-벡터 연산을 수행합니다. $$y \leftarrow \alpha A x + \beta y$$
  • 레벨 3 BLAS는 행렬-행렬 연산을 수행합니다. $$C \leftarrow \alpha AB + \beta C$$

위의 연산들은 선형대수에서 매우 기초적인 연산들이고, 이러한 연산을 수행하는 속도를 빠르게할 수 있다면 전반적인 계산 속도를 빠르게할 수 있을 것입니다.

BLAS는 1979년 Fortran 라이브러리로 시작되었습니다. 이 인터페이스는 netlib 웹사이트에서 BLAS 기술(BLAST) 포럼에 의해 표준화되었습니다. 이 Fortran 라이브러리는 표준 BLAS 라이브러리로 불리게 됩니다.

특징

선형대수 연산을 사용하는 대부분의 라이브러리는 BLAS 라이브러리를 활용하고 있으며, 일반적으로 사용자는 BLAS 라이브러리를 신경 쓸 필요가 없습니다. 그렇다면 이 포스트에서 BLAS를 소개하는 이유는 무엇일까요?

실제 사용되는 많은 BLAS 라이브러리는 벡터 레지스터 또는 SIMD 명령어와 같은 특수 부동 소수점 하드웨어를 활용하도록 구현되어 있습니다. CPU를 활용한 BLAS 라이브러리에는 OpenBLAS, BLIS, ATLAS, 인텔의 MKL, 애플의 vecLib 등이 있습니다. GPU를 활용한 BLAS 라이브러리에는 Nvidia 그래픽카드의 cuBLAS, AMD 그래픽카드의 rocBLAS 등이 있습니다. 특정 시스템에 맞춰 최적화된 BLAS를 잘 활용하면 상당한 성능 이점을 얻을 수 있습니다.

BLAS in R

R에서 사용중인 BLAS는 sessionInfo() 명령어를 통해 확인할 수 있습니다.

다음은 제 개인 컴퓨터(MacBook Pro 14-inch, 2021)의 환경입니다12.

1

sessionInfo()

R version 4.1.2 (2021-11-01)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Monterey 12.3

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.1-arm64/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.1-arm64/Resources/lib/libRlapack.dylib

locale:
[1] en_US.utf-8/en_US.utf-8/en_US.utf-8/C/en_US.utf-8/en_US.utf-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

loaded via a namespace (and not attached):
[1] compiler_4.1.2 jsonlite_1.7.2 rlang_0.4.12

인텔 CPU를 활용하는 저희 연구실의 계산 서버(Linux)에서는 인텔 MKL 라이브러리를 활용해 가속한 R을 사용하고 있습니다.

1

sessionInfo()

R version 4.1.2 (2021-11-01)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: CentOS Linux 7 (Core)

Matrix products: default
BLAS/LAPACK: /opt/intel/compilers_and_libraries_2020.4.304/linux/mkl/lib/intel64_lin/libmkl_gf_lp64.so

locale:
 [1] LC_CTYPE=en_US.utf-8       LC_NUMERIC=C              
 [3] LC_TIME=en_US.utf-8        LC_COLLATE=en_US.utf-8    
 [5] LC_MONETARY=en_US.utf-8    LC_MESSAGES=en_US.utf-8   
 [7] LC_PAPER=en_US.utf-8       LC_NAME=C                 
 [9] LC_ADDRESS=C               LC_TELEPHONE=C            
[11] LC_MEASUREMENT=en_US.utf-8 LC_IDENTIFICATION=C       

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

loaded via a namespace (and not attached):
[1] compiler_4.1.2

맥에서 R의 BLAS 변경하기

맥의 BLAS

안타깝게도, 제가 현재 사용하고 있는 ARM 아키텍쳐 기반의 맥에서는 인텔의 MKL 라이브러리를 사용할 수 없습니다. 이는 아키텍쳐를 변경하는데서 온 피할 수 없는 결과이기도 합니다.

다행히 애플(Apple)에서는 Accelerate라는, 자체적으로 최적화한 프레임워크(Framework)를 제공하고 있습니다.

페이지에서 소개하듯, 이 프레임워크는 아이폰부터 맥까지 다양한 환경에서 작동하기에 제 컴퓨터에서도 작동할 것이라 기대할 수 있었습니다.

R의 BLAS 변경

CRAN의 공식 FAQ 사이트에서 맥에서 R의 BLAS를 변경하는 방법에 대해 안내하고 있습니다. 다음의 명령어를 입력하면 됩니다.

1
2
3
4

cd /Library/Frameworks/R.framework/Resources/lib

# for vecLib use
ln -sf libRblas.vecLib.dylib libRblas.dylib

여기서 vecLib은 Accelerate 프레임워크에서 제공하는 BLAS 라이브러리의 이름입니다. 이 명령어를 실행하고 나면 sessionInfo()의 결과에서 더 이상 BLAS의 정보가 표시되지 않습니다.

1

sessionInfo()

R version 4.1.2 (2021-11-01)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Monterey 12.3

Matrix products: default
LAPACK: /Library/Frameworks/R.framework/Versions/4.1-arm64/Resources/lib/libRlapack.dylib

locale:
[1] en_US.utf-8/en_US.utf-8/en_US.utf-8/C/en_US.utf-8/en_US.utf-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

loaded via a namespace (and not attached):
[1] compiler_4.1.2 jsonlite_1.7.2 rlang_0.4.12

다시 원래의 BLAS로 돌아가려면 다음을 입력하면 됩니다.

1
2
3
4

cd /Library/Frameworks/R.framework/Resources/lib

# for R reference BLAS use
ln -sf libRblas.0.dylib libRblas.dylib

성능 비교

실제 표준 BLAS를 사용한 R과(이하 reference) BLAS 라이브러리 변경 후 R의(이하 vecLib) 성능 비교를 실시해보았습니다.

단순 행렬 곱셈 비교

$1000 \times 1000$ 행렬의 곱셈에 대한 결과를 비교해보았습니다. microbenchmark 패키지를 활용했습니다.

1
2
3
4
5

set.seed(100)
n = 1000
A = matrix(rnorm(n * n), n, n)
B = matrix(rnorm(n * n), n, n)
microbenchmark::microbenchmark(C = A %*% B)

reference의 결과입니다.

Unit: milliseconds
 expr      min       lq     mean   median      uq      max neval
    C 319.5581 320.6043 325.0342 322.0135 327.045 349.8612   100

vecLib의 결과입니다.

Unit: milliseconds
 expr      min       lq   mean   median       uq      max neval
    C 4.542349 4.633513 5.0977 4.676419 5.108026 7.333506   100

매우 큰 성능 향상이 있음을 확인할 수 있습니다.

benchmarkme 패키지 결과 비교

이번에는 benchmarkme 패키지를 활용해 속도를 비교해보겠습니다.

1

res <- benchmarkme::benchmark_std(runs = 5)

reference의 결과입니다.

# Programming benchmarks (5 tests):
        3,500,000 Fibonacci numbers calculation (vector calc): 0.106 (sec).
        Grand common divisors of 1,000,000 pairs (recursion): 0.217 (sec).
        Creation of a 3,500 x 3,500 Hilbert matrix (matrix calc): 0.141 (sec).
        Creation of a 3,000 x 3,000 Toeplitz matrix (loops): 0.599 (sec).
        Escoufier's method on a 60 x 60 matrix (mixed): 0.598 (sec).
# Matrix calculation benchmarks (5 tests):
        Creation, transp., deformation of a 5,000 x 5,000 matrix: 0.219 (sec).
        2,500 x 2,500 normal distributed random matrix^1,000: 0.11 (sec).
        Sorting of 7,000,000 random values: 0.598 (sec).
        2,500 x 2,500 cross-product matrix (b = a' * a): 9.47 (sec).
        Linear regr. over a 5,000 x 500 matrix (c = a \ b'): 0.79 (sec).
# Matrix function benchmarks (5 tests):
        Cholesky decomposition of a 3,000 x 3,000 matrix: 5.17 (sec).
        Determinant of a 2,500 x 2,500 random matrix: 1.76 (sec).
        Eigenvalues of a 640 x 640 random matrix: 0.422 (sec).
        FFT over 2,500,000 random values: 0.0824 (sec).
        Inverse of a 1,600 x 1,600 random matrix: 1.43 (sec).

vecLib의 결과입니다.

# Programming benchmarks (5 tests):
        3,500,000 Fibonacci numbers calculation (vector calc): 0.095 (sec).
        Grand common divisors of 1,000,000 pairs (recursion): 0.236 (sec).
        Creation of a 3,500 x 3,500 Hilbert matrix (matrix calc): 0.136 (sec).
        Creation of a 3,000 x 3,000 Toeplitz matrix (loops): 0.593 (sec).
        Escoufier's method on a 60 x 60 matrix (mixed): 0.397 (sec).
# Matrix calculation benchmarks (5 tests):
        Creation, transp., deformation of a 5,000 x 5,000 matrix: 0.216 (sec).
        2,500 x 2,500 normal distributed random matrix^1,000: 0.111 (sec).
        Sorting of 7,000,000 random values: 0.602 (sec).
        2,500 x 2,500 cross-product matrix (b = a' * a): 0.0438 (sec).
        Linear regr. over a 5,000 x 500 matrix (c = a \ b'): 0.0078 (sec).
# Matrix function benchmarks (5 tests):
        Cholesky decomposition of a 3,000 x 3,000 matrix: 0.109 (sec).
        Determinant of a 2,500 x 2,500 random matrix: 0.131 (sec).
        Eigenvalues of a 640 x 640 random matrix: 0.204 (sec).
        FFT over 2,500,000 random values: 0.0834 (sec).
        Inverse of a 1,600 x 1,600 random matrix: 0.121 (sec).

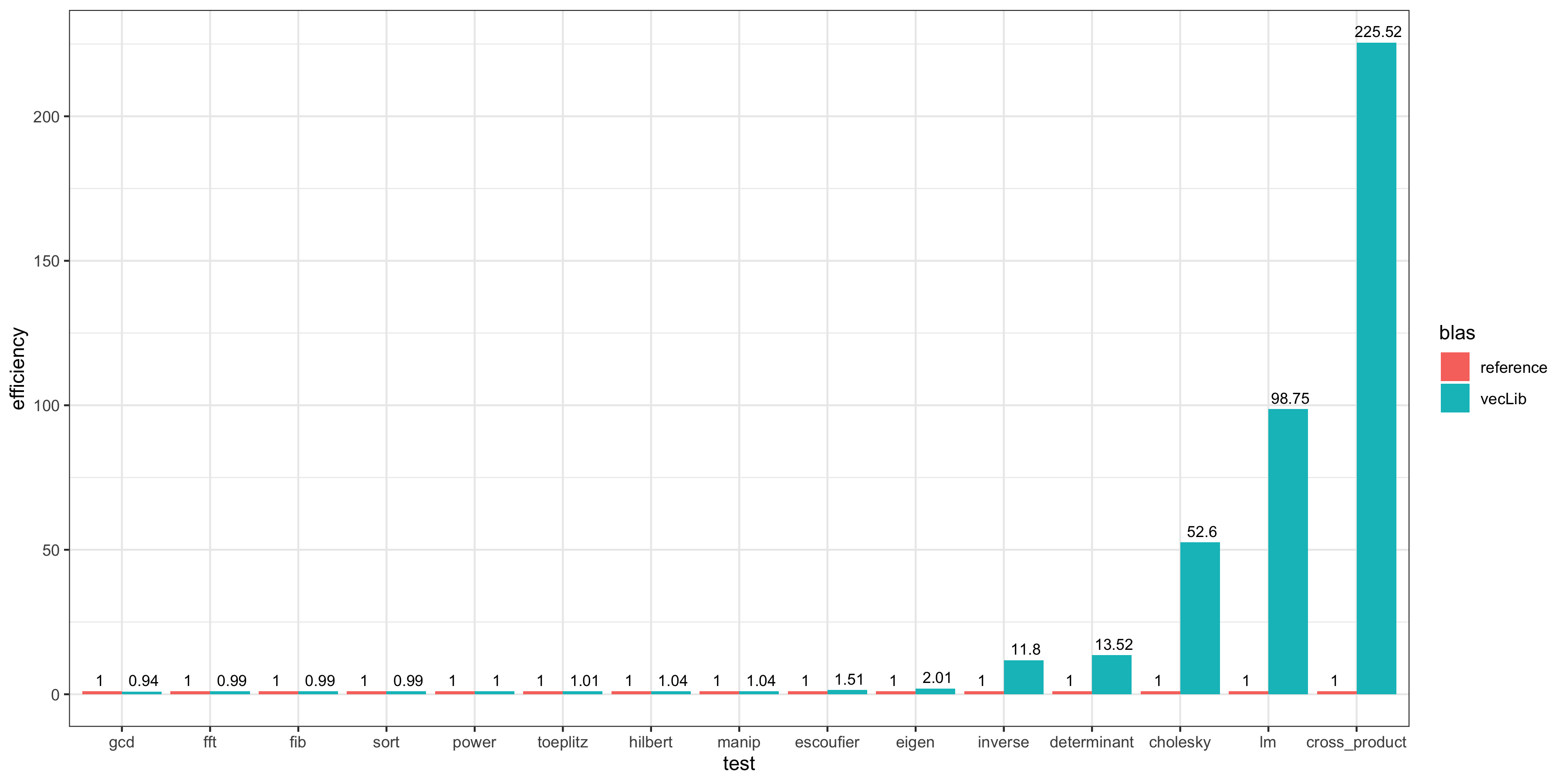
결과를 시각화하였습니다.

reference에서 걸린 시간의 중앙값을 1이라고 하였을 때, vecLib이 걸린 시간의 중앙값의 역수를 효율성(efficiency)으로 계산해 그 값을 시각화하였습니다. 행렬 연산을 사용하는 함수에서 매우 효율적인 결과를 보여줍니다.

다만 이 결과는 매우 제한적인 실험에서의 것이며 실제 환경에서는 위와 같이 큰 차이를 보이지는 않았습니다. 제 경험에 따르면 관측치 수 10,000개 정도를 다루는 선형 회귀모형에서는 약 2배 정도 빠른 결과를 보여주었으며 행렬 계산이 잦은 MCMC 시뮬레이션에서는 그 이상의 성능 향상을 보여주었습니다.

여담

애플의 M1 칩에는 AMX: Apple Matrix Coprocessor 라는 행렬 계산에 특화된 하드웨어 가속기가 탑재되어 있으며 Accelerate framework은 이를 활용한다고 알려져있습니다.

Source: https://www.apple.com/kr/newsroom/2020/11/apple-unleashes-m1/

Source: https://www.apple.com/kr/newsroom/2020/11/apple-unleashes-m1/

그래서일까요? 적당히 최적화된 라이브러리를 사용하는 환경에서는 이전에 사용하던 iMac보다 현재 M1에서의 R, Python 속도가 훨씬 빠르게 느껴집니다. 물론 MKL 라이브러리를 사용하고 48 코어 96 스레드가 탑재된 계산서버보다는 느리지만 전력 소모량을 생각해보면 마법과 같다 생각될 정도입니다.

관심이 있으신 분들은 다음의 자료들을 읽어보시기 바랍니다.

참고자료

  1. 기본으로 제공되는 libRblas.0.dylib는 표준 BLAS 라이브러리로 알고 있습니다. ↩︎

  2. 맥의 패키지 관리자인 homebrew를 사용해 설치한 R은 기본으로 OpenBLAS를 사용하는 것으로 알고 있습니다. ↩︎

comments powered by Disqus
CATALOG
    FEATURED TAGS
    bayesian r statistics