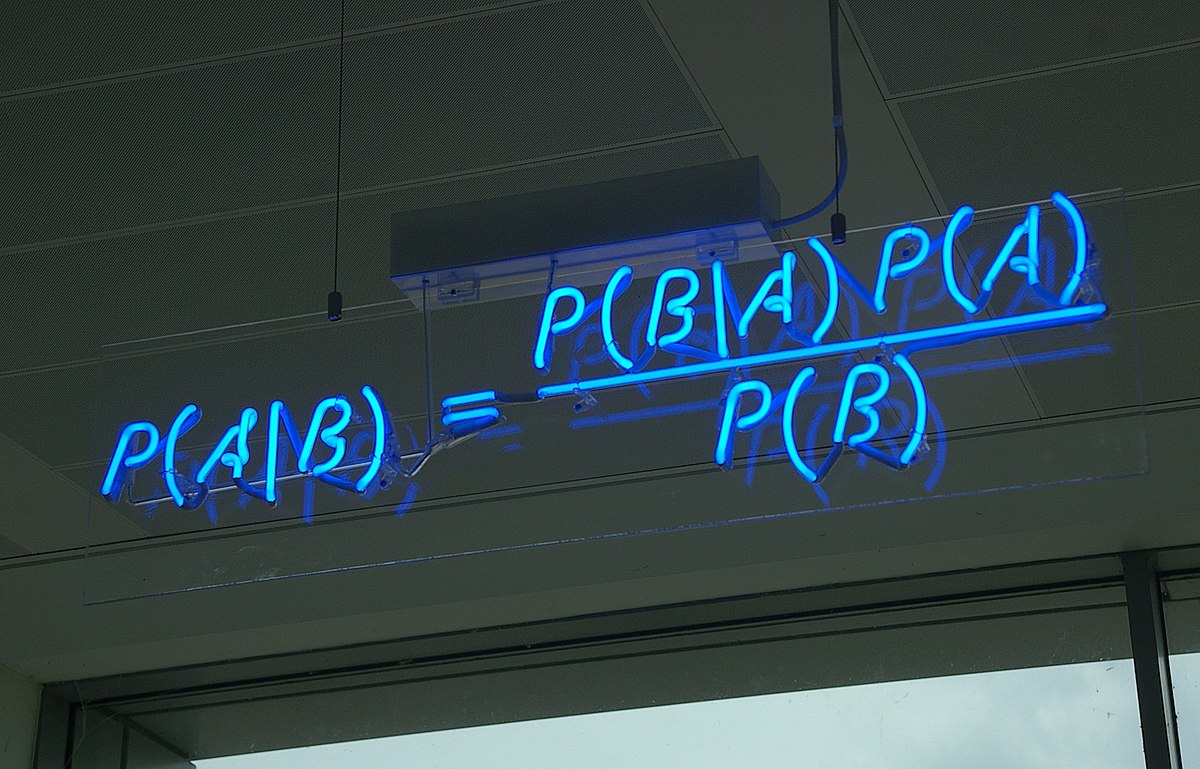if your experiment needs statistics you ought to have done a better experiment
- Ernest Rutherford
통계적 추론
도입
머신러닝의 문제는 통계적 모형의 모수(parameter)를 추정(estimate)하는 문제라 할 수 있습니다. 자료가 주어지면 모형을 세우고, 적당한 알고리듬으로 모형의 모수를 추정하여 미지의 자료(test data)에 일반화하는 것이죠.
통계적 추론(statistical inference)에는 크게 두 가지 접근이 있습니다. 하나는 고전적(classical) 또는 빈도적 추론(frequentist inference)이며 하나는 베이즈 추론(Bayesian inference)입니다.
통계적 추론에서는 일반적으로 다음을 가정합니다.
- 모수가 주어져 있을 때, 서로 독립이고 동일한 분포 $p(x|\theta)$를 따르는(independent and identically distributed; i.i.d.) 자료 (data) $D = \{x_1, x_2, \cdots, x_N\}$.
- 자료의 분포를 결정하는 모수(parameter) $\theta$
빈도적 추론
빈도적 추론(frequentist inference)에서는 모수 $\theta$가 고정된 상수라 생각합니다. 자료 $D$로부터 $\theta$의 점추정량 $\hat{\theta}$를 계산하거나 구간 추정으로 신뢰 구간(confidence interval)을 계산하기도 합니다. 대수의 법칙(law of large numbers)은 추정량 $\hat{\theta}$이 실제 모수 $\theta$에 충분히 가까워짐(consistency)을 보장합니다.
베이즈 추론
베이즈 추론(Bayesian inference)에서는 모수 $\theta$를 확률변수(random variable)이라 생각합니다. 자료 $D$로부터 모수의 확률분포를 계산하고, 이를 바탕으로 점추정량을 계산하거나 구간 추정으로 신뢰 구간(Bayesian confidence interval, or credible interval)을 계산합니다.
베이즈 추론의 이론적 정당화는 De Finetti 등에 의해 이루어져 왔으며, 빈도적 추론에서와 비슷하게 자료의 수가 충분히 클 때 모수의 확률분포의 수렴성에 대한 이론들이 연구되어 왔습니다.
빈도적 추론과 비교했을 때 베이즈 추론은 적은 수의 표본으로도 통계적 추론이 가능하고, 신뢰구간이나 유의확률을 자연스럽게 정의할 수 있다는 강점이 있습니다.
통계적 분석의 단계
통게적 모형으로 데이터를 분석하기 위한 과정은 크게 다음과 같습니다.
- 분석 계획 설정 및 데이터 수집 (Plan)
- 배경지식 수집: 해당 분야에서 자주 사용하는 가정과 분석 방법, 시각화 방법 등을 조사합니다.
- 문제 설정: 자료로부터 얻고 싶은 정보를 정리합니다. 그렇게 얻은 정보를 가공하는 방법(시각화 등)에 대해서도 생각해두는 것이 좋습니다.
- 분석 계획: 어떤 방법을 사용할 지, 어떤 절차를 따를 것인지 (If This Then That; IFTTT)를 간단히 생각합니다.
- 데이터 수집: 분석 계획에 맞게 데이터를 수집합니다.
- 데이터 (Data)
- 데이터 전처리: 결측치(missing value)를 처리하고, 정규화 등의 과정으로 변수를 가공합니다.
- 탐색적 자료 분석: 시각화, 수치적 요약값 등을 확인하여 자료에 대한 간단한 분석을 실시합니다.
- 데이터 전처리와 탐색적 자료분석은 유기적으로 함께 실시합니다.
- R에서는
dplyr,ggplot2등의 패키지를 활용해 데이터 처리 과정을 쉽게 진행할 수 있습니다. Python에서는pandas,seaborn등의 패키지를 사용하시면 됩니다.
- 통계적 모형화 (Modeling)
- 자료를 생성하는 메커니즘(모형)을 생각하여 확률분포로 나타냅니다.
- 탐색적 자료 분석 과정에서 얻은 자료에 대한 정보와 배경지식을 결합하여 효율적인 모형을 구현할 수 있습니다.
- 세운 모형을 수식으로 나타냅니다.
- 모형 적합 (Fitting)
- (R, Stan 코드를 작성해) 모형을 구현하고 매개변수를 추정합니다.
- 결과 해석 (Result)
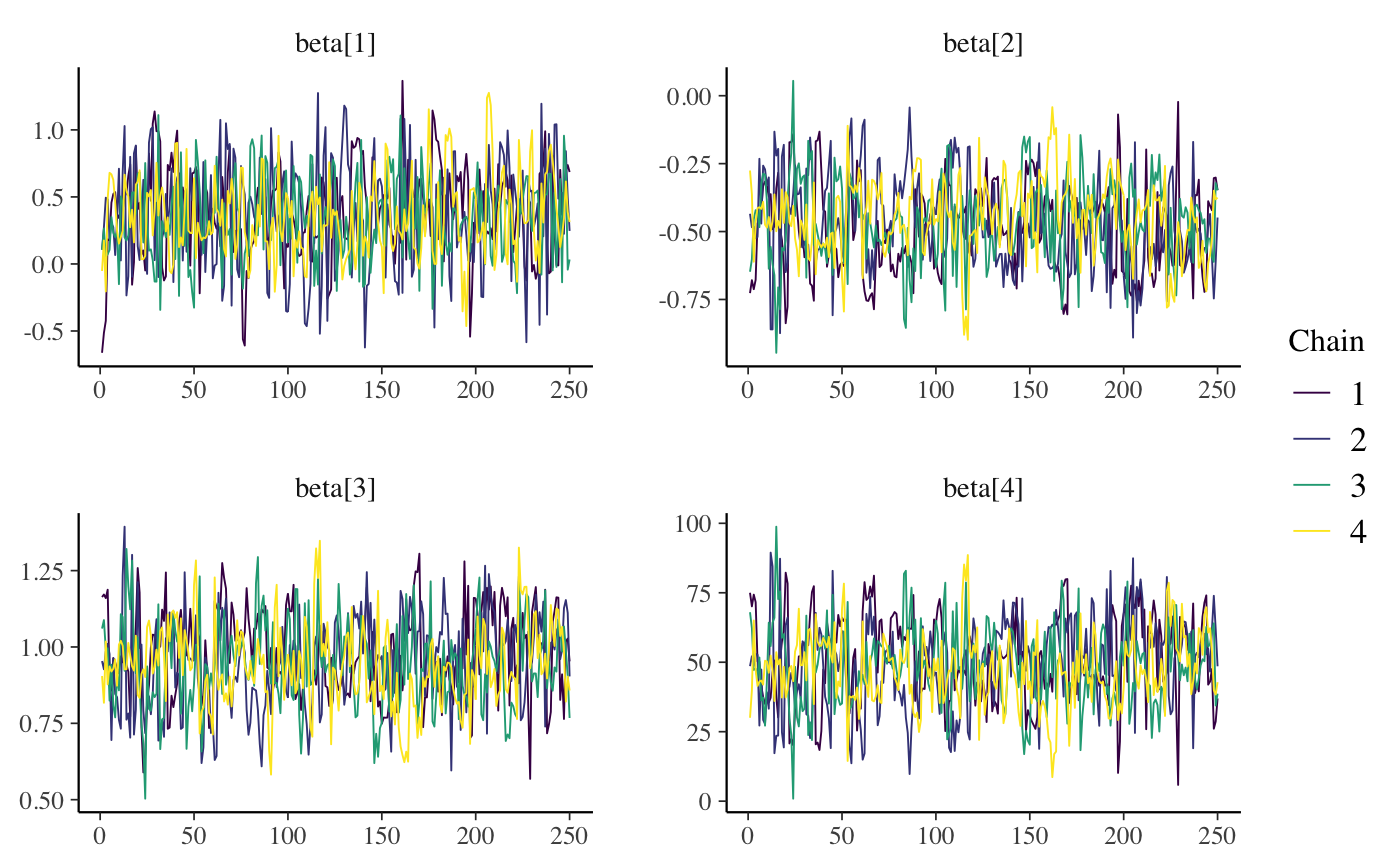
- Stan을 사용했다면 MCMC 표본의 수렴진단(diagnosis)을 실시합니다.
- 적합된 모형의 모수를 확인하여 자료의 경향성을 확인하거나 새로운 값에 대한 예측(prediction)을 실시합니다.
- 원하는 수준의 결과를 얻지 못했다면 다시 1로 돌아갑니다1.
이 외에도 자료나 모형, 사전 분포, 컴퓨팅 환경 등을 바꾸어도 같은 결과가 나오는 지와 같은 재현성(reproducibility) 확인 또한 중요한 작업입니다.
베이즈 추론
베이즈 추론의 3요소
베이즈주의자(Bayesian)들은 모든 불확실성을 확률로 표현 가능하다는 가정 아래 모형 $f(\cdot | \theta)$와 모수 $\theta$에 확률분포를 생각합니다. 다음의 확률분포를 베이즈 추론의 3요소라 부릅니다.
- 사전분포(prior distribution): 모수에 대한 기존의 지식을 담고 있는 분포입니다. $$\theta \sim \pi(\theta), \quad \theta \in \Theta.$$
- 모형(model): 모수에 대한 관측치로부터의 정보를 담고 있는 분포입니다. $$X|\theta \sim f(x|\theta)$$ 가능도(likelihood) $f(\theta; x)$는 $f(x|\theta)$를 주어진 $x$에 대하여 $\theta$의 함수로 본 것으로 이해할 수 있습니다.
- 사후분포 (posterior distribution): 모수에 대한 기존의 지식에 관측치로부터의 정보를 반영한, 모수에 대한 모든 정보를 담고 있는 분포입니다.
$$ \theta|X \sim \pi(\theta|X) $$
베이즈 법칙
베이즈 법칙(Bayes’ rule)은 사후분포를 계산하기 위한 식으로 다음과 같이 주어집니다.
$$ \begin{equation} \pi(\theta | x) = \frac{\pi(\theta) f(x|\theta)}{m(x)}, \quad m(x) = \int_\Theta \pi(\theta) f(x|\theta) d\theta \end{equation} $$
$m(x)$를 $X$의 주변분포(marginal ditribution)라 부릅니다.
여기서 우변의 분모, 주변분포는 $\theta$에 의존하지 않으므로 베이즈 법칙을 다음과 같이 요약할 수 있습니다.
$$ \pi(\theta | x) \propto \pi(\theta) f(x|\theta), $$
또는,
$$\texttt{사후분포} \propto \texttt{사전분포} \times \texttt{가능도}$$
베이즈 추정량
앞서 사후분포는 모수에 대한 모든 정보를 담고 있다고 말씀드렸습니다. 베이즈 추정량(Bayes estimator)란 사후분포를 한 점으로 요약한 통계량으로 대표적으로 다음과 같이 정의되는 사후평균(posterior mean) 또는 사후기댓값(posterior expectation)이 있습니다.
$$ \begin{equation} \hat{\theta}^{mean} = \argmin_a \mathbb{E}[ (\theta-a)^2 | x] \end{equation} $$
사후분포로 $\pi(\theta|x)$로부터 사후평균은 다음과 같이 계산할 수 있습니다.
$$ \begin{equation} \hat{\theta}^{mean} = \mathbb{E}[\theta | x] = \int_\Theta \theta \pi(\theta|x) d\theta \end{equation} $$
이 외에도 사후중앙값(posterior median) $\hat{\theta}^{med}$, 사후최빈값(maximum a posteriori; MAP) $\hat{\theta}^{MAP}$와 같은 값을 사용하기도 합니다.
에측
통계적 추론에서 반응변수 값에 대한 추정을 예측(prediction)이라 합니다.
머신러닝에서 훈련 자료 $D = \{ D_i = (\mathbf{x}_i, y_i), i=1,2, \cdots, n\}$가 있을 때, 실제 모형이 $$p(y|\mathbf{x}, \theta)$$라 하겠습니다. 즉, $$f(D_i|\theta) = p(y_i | \mathbf{x}_i, \theta), \quad \theta \sim \pi(\theta) $$ 라 하겠습니다. 새로운 자료 $\mathbf{x}^\ast$에 대한 예측분포 $p(y^\ast | \mathbf{x}^\ast, D)$는 다음과 같이 계산할 수 있습니다.
$$ \begin{equation} \begin{aligned} p(y^\ast | \mathbf{x}^\ast, D) &= \int p(y^\ast, \theta | \mathbf{x}^\ast, D) d\theta \\ &= \int p(y^\ast | \theta, \mathbf{x}^\ast, D) p(\theta | \mathbf{x}^\ast, D) d\theta \\ &= \int p(y^\ast | \theta, \mathbf{x}^\ast) p(\theta | D) d\theta \end{aligned} \end{equation} $$
첫 등식은 전확률법칙(total probability law)으로부터, 두 번째 등식은 확률의 곱셈벅칙으로부터, 세 번째 등식은 조건부 독립성(conditional independency)에 의해 성립합니다. 즉, 우리가 사후분포를 계산할 수 있다면 모수에 대한 추론과 새로운 자료에서의 예측이 모두 가능합니다.
계산 문제
베이즈 추론에서 가장 어려움을 겪는 부분은 적분의 계산이라 할 수 있습니다. 사후분포를 정확히 계산하기 위해서는 분모의 주변분포를 위한 적분을 계산해야하며 베이즈 추정량, 예측분포의 계산 등에서도 $\Theta$의 차원(dimensionality) 만큼의 다차원 적분을 계산해야 합니다.
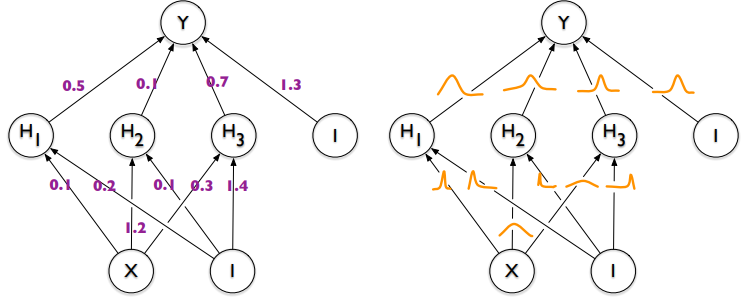
Standard DNN and Bayesian DNN, figure from Blundell, Charles, et al. "Weight uncertainty in neural network." International conference on machine learning. PMLR, 2015.
가령, 베이즈 딥러닝 모형(Bayesian deep learning model)에서 각 가중치(weight)에 사전분포를 부여한다고 하면 그 갯수만큼의 적분을 계산해야하는데 이것은 현실적으로 불가능합니다.
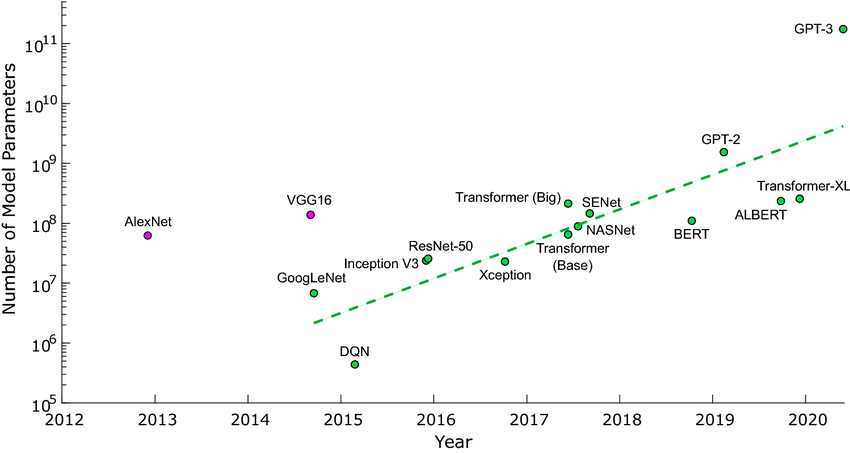
Number of parameters in recent landmark neural networks, figure from Bernstein, Liane, et al. "Freely scalable and reconfigurable optical hardware for deep learning." Scientific reports 11.1 (2021): 1-12.
켤레사전분포
이 문제를 피하기 위해 사용되던 고전적인 방법은 ‘계산이 쉬운 분포를 사용하는 것’이었습니다. 켤레사전분포(conjuagte prior)이라 불리는 사전분포와 모형을 사용하면 사후분포를 쉽게 계산할 수 있습니다.
근사 베이즈 계산
그러나 켤레사전분포를 사용하는 것은 모형의 형태에 제약이 커 실제 자료에 적용하기가 어렵습니다. 때문에 근사적으로 사후분포를 계산하고 이에 대한 추론을 실시하는 방법들이 제안되어 왔습니다. 이 방법에는 크게 두 가지 접근이 있습니다.
- 결정적(deterministic) 근사 - 변분 추론(variational inference), 라플라스 근사(Laplace approximation)와 같은 방법들은 사후분포와 가장 가까운 특정 분포들을 찾아 이 분포를 바탕으로 베이즈 추론을 실시합니다.
- 확률적(stochastic) 근사 - HMC, Gibbs sampler와 같은 MCMC(Marko chain Monte Carlo) 알고리듬을 이용하면 사후분포에서 표본을 추출하고, 이를 바탕으로 베이즈 추론을 실시할 수 있습니다.
확률적 근사는 충분히 많은 표본을 통해 참값을 계산할 수 있다(unbiased)는 장점이 있지만, 계산이 어렵다는 단점을 가지고 있습니다. 반면에, 결정적 근사는 계산(최적화)이 상대적으로 간편하다는 장점이 있지만, 참값을 계산할 수 없다(biased)는 단점을 가지고 있습니다.
Steps for Bayesian inference (Gelman 2013)
The process of Bayesian data analysis can be idealized by dividing it into the following three steps:
- Setting up a full probability model—a joint probability distribution for all observable and unobservable quantities in a problem. The model should be consistent with knowledge about the underlying scientific problem and the data collection process.
- Conditioning on observed data: calculating and interpreting the appropriate posterior distribution—the conditional probability distribution of the unobserved quantities of ultimate interest, given the observed data.
- Evaluating the fit of the model and the implications of the resulting posterior distribution: how well does the model fit the data, are the substantive conclusions reasonable, and how sensitive are the results to the modeling assumptions in step 1? In response, one can alter or expand the model and repeat the three steps.
참고자료
- Hoff, P. D. (2009). A first course in Bayesian statistical methods (Vol. 580). New York: Springer.
- Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013). Bayesian data analysis. CRC press.
- 겐타로마쓰우라. 데이터 분석을 위한 베이지안 통계 모델링 with Stan & R: 현재를 해석하고 미래를 예측하자! (주)도서출판길벗. https://books.google.co.kr/books?id=LjqRDwAAQBAJ
이 과정을 두려워하는 분들이 처음부터 너무 복잡한 모형을 가정하는 경우가 많습니다. 그러나 너무 복잡한 모형은 구현과 추정이 모두 어렵기 때문에 분석이 제대로 이루어지지 않을 수 있습니다. 가급적이면 간단한 모형에서부터 순서대로 모형을 적합해나가는 것을 권장합니다. 간단한 모형이란 ‘설명 변수의 수가 적고’, ‘변수 간의 복잡한 관계를 덜 고려하는’ 모형을 의미합니다. ↩︎
comments powered by Disqus