statistics Bayesian

베이즈 통계학 소개 - (1)

Posted by Kyeongwon Lee on Sunday, July 10, 2022

서론

최근 지인분으로부터 ‘베이즈 통계학이 기존의 통계학과 어떻게 다른지’, ‘왜 베이즈 통계학을 공부해야 하는지’, ‘비교적 간단한 예제를 빈도론 통계로 접근한 경우와 베이즈 통계로 접근한 경우의 비교’, ‘그 밖에 일반인들이 베이즈 통계가 왜 필요한지 확 와 닿게 하는 내용’에 대한 질문을 받았습니다.

이 분께 답장을 보내드리며 스스로도 많은 공부를 하게 되었고, 비슷한 궁금증을 가지신 분이 많을 것 같아 관련 내용을 공개적으로 정리해보려 합니다. 이전에도 비슷한 내용을 다루기는 했지만, 조금 더 상세히 작성하겠습니다.

베이즈 추론

베이즈 추론(Bayesian inference)은 ‘주관적 확률과 베이즈 정리에 기반한 통계적 추론’입니다. 이 글에서는 ‘주관적 확률’, ‘베이즈 정리’, ‘통계적 추론’에 대해 소개하겠습니다.

주관적 확률

주사위를 던졌을 때, 1이 나올 확률은 1/6이다.

위의 문장에서 ‘확률’이란 무엇일까요? 확률을 바라보는 여러 관점들에 대해 소개합니다.

고전적 확률

“The theory of chance consists in reducing all the events of the same kind to a certain number of cases equally possible, that is to say, to such as we may be equally undecided about in regard to their existence, and in determining the number of cases favorable to the event whose probability is sought. The ratio of this number to that of all the cases possible is the measure of this probability, which is thus simply a fraction whose numerator is the number of favorable cases and whose denominator is the number of all the cases possible”

  • Pierre Simon Laplace

확률의 고전적 정의는 각 사건이 모두 동일한 정도로 기대된다는 가정에서 시작합니다. 각 사건이 동일한 정도로 기대되고 동시에 일어날 수 없을 때, 고전적 확률은 다음과 같이 정의됩니다. $$P = \frac{\textrm{특정 사건이 일어나는 경우의 수}}{\textrm{일어날 수 있는 모든 경우의 수}}$$

사건 $A$가 일어날 확률을 $P(A)$라 쓰고, 이 값은 다음과 같이 계산할 수 있습니다. $$P(A) = \frac{\textrm{사건 $A$가 일어나는 경우의 수}}{\textrm{일어날 수 있는 모든 경우의 수}}$$

가령, 공정한 주사위를 던졌을 때 1이 나올 확률은 1/6입니다. 고전적 확률은 객관적으로, 연역적으로 확률을 계산합니다.

빈도론 확률

빈도론 확률(frequentist probability)에서는 확률을 어떤 사건을 반복하였을 때 일어나는 상대 빈도수로 정의합니다.

어떤 사건이 일어날 상대빈도는 다음과 같습니다.

$$\dfrac{\textrm{특정 사건이 관측된 횟수}}{\textrm{모든 사건이 관측된 횟수}}$$

빈도론 확률은 동일한 실험이 무한번 반복되는 것을 상정하고, 확률을 사건의 상대빈도로 정의합니다. 가령, 주사위를 던졌을 때 1이 나올 확률이 1/6이라는 것은 주사위를 무한 번 던지면 그 중 1/6 정도의 비율로 1이 나온다는 것을 의미합니다.

빈도론 확률은 객관적으로, 경험적으로, 귀납적으로 확률을 계산합니다. 빈도론 확률은 확률이 주관적으로 정의되는 것이 아닌, 자연현상의 성질에 의해 결정되는 값으로 생각합니다.

확률의 빈도론 해석을 바탕으로 하는 통계적 추론을 빈도론 추론(frequentiest inference)이라 합니다. 대표적인 빈도론 추론 방법론으로 최대가능도추정, 가능도비검정(Z-test, T-test, F-test) 등이 있습니다. Fisher, Neyman 등에 의해 발전해왔습니다.

주관적 확률

확률을 지식 또는 개인의 믿음의 정도로 해석하는 확률론을 주관적 확률(subjective probability)이라 합니다. 가령, 주사위를 던졌을 때 1이 나올 확률이 1/6이라는 것은 분석자가 주사위를 던졌을 때 1이 나올 것이라 기대하는 믿음의 정도가 1/6이라는 것입니다. 1, 2, 3, 4, 5, 6에 대한 확률이 모두 1/6이라는 것은 ‘이 주사위는 공정하다’는 믿음을 반영한 것이라 생각할 수 있습니다.

주관적 확률론에서는 분석자에 따라 어떤 사건이 발생할 확률이 달라질 수 있습니다. 주관적 확률에 대한 이론적 정당화는 De Finetti, L. J. Savage, Richard T. Cox 등에 의해 이루어져 왔습니다.

예 - 일기예보 문제

2022년 7월 서울시 관악구 신림동의 주간예보

2022년 7월 서울시 관악구 신림동의 주간예보

대기상태(기온, 습도 등) $x$ 가 주어졌을 강수확률을 $f(x)$로 나타내는 모형을 생각해보겠습니다.

어느 날 기상청에서 $f(x) = 0.7$로 계산되었다면 0.7의 확률로 오늘은 비가 내리고 0.3의 확률로 비가 내리지 않는다고 예보할 것입니다.

비가 내릴 확률이 0.7이란?

  • 빈도론 확률의 해석: “같은 대기상태의 날이 무한히 많이 반복된다면, 그 중 70% 정도는 비가 내릴 것이다.”
  • 주관적 확률의 해석: “오늘 비가 올 것이라는 우리의 (합리적) 믿음이 70% 정도이다.”

여러분은 어떤 해석이 더 자연스러우신가요?

베이즈 정리

이번에는 베이즈 정리(Bayes’ theorem)을 소개하겠습니다. 두 사건 $A$, $B$에 대해 베이즈 정리는 다음과 같이 주어집니다.

\begin{equation} P(B|A) = \frac{P(A | B) P(B)}{P(A)} \end{equation}

여기서 $P(A)$는 어떤 사건 $A$가 일어날 확률을, $P(A|B)$는 사건 $B$가 일어났을 때 $A$가 일어날 확률(조건부 확률)을 의미합니다. 베이즈 정리는 정말 중요한 정리로, 다음과 같은 의미를 갖습니다.

  1. 역확률 문제: $P(B | A)$를 알고 있을 때, $P(A | B)$를 계산할 수 있다.
  2. 지식의 갱신: 이전의 지식($P(A)$)에 현재의 정보($P(B | A)$)를 반영하여 지식을 갱신 ($P(A | B)$)할 수 있다.

예 - 코로나 감염 예측 문제

어떤 코로나 검사는 실제 코로나 바이러스에 감염된 사람의 90%를 환자로 분류하고, 감염되지 않은 사람의 10%를 환자로 분류한다는 것이 알려져 있습니다. 실제 코로나 바이러스의 감염률이 5%라는 것이 알려져 있다고 했을 때, 베이즈 정리는 다음의 질문들에 대한 답을 줍니다.

역확률 문제: 어떤 사람이 검사 결과 코로나 바이러스 감염 환자로 분류되었을 때, 실제 코로나 바이러스에 감염되었을 확률은 얼마인가?

어떤 사람이 검사에서 환자로 분류될 사건을 $A$, 코로나 바이러스에 감염되는 사건을 $B$라고 하겠습니다. 그러면 $$P(B|A) = \frac{P(A|B)P(B)}{P(A)} = \frac{P(A|B)P(B)}{P(A|B)P(B) + P(A|B^c)P(B^c)}$$ 에서

1
2
3
4
5
6
7

b <- 0.05
not_b <- 1 - b
a_given_b <- 0.9
a_given_not_b <- 0.1

prob <- a_given_b * b / (a_given_b * b + a_given_not_b * not_b) 
print(prob)

[1] 0.3214286

입니다. 즉, 실제 코로나 바이러스에 감염되었을 확률은 32.14% 정도임을 알 수 있습니다. 즉, 베이즈 정리를 사용하면 사건의 발생 순서(감염 $\rightarrow$ 진단)를 뒤집은(진단 $\rightarrow$ 감염) 역확률을 계산할 수 있다.

지식의 갱신: 내가 환자로 분류되었을 때, 실제로 감염되었을 확률은 어떻게 바뀌었는가?

  • 기존에는 아무런 정보가 없었기에, 내가 코로나 바이러스에 감염될 확률을 5% 정도라고 믿었습니다. ($P(A)$)
  • 코로나 검사에서 내가 환자로 분류되었습니다. ($P(B | A)$)
  • 코로나 검사로부터 내가 코로나에 감염되었을 확률을 32.14%로 갱신합니다. ($P(A | B)$)

베이즈 정리를 사용하여 기존의 믿음(코로나 바이러스에 감염된 확률)에 현재의 정보를 반영하여 믿음을 갱신 ($P(A | B)$)할 수 있습니다.

통계적 추론

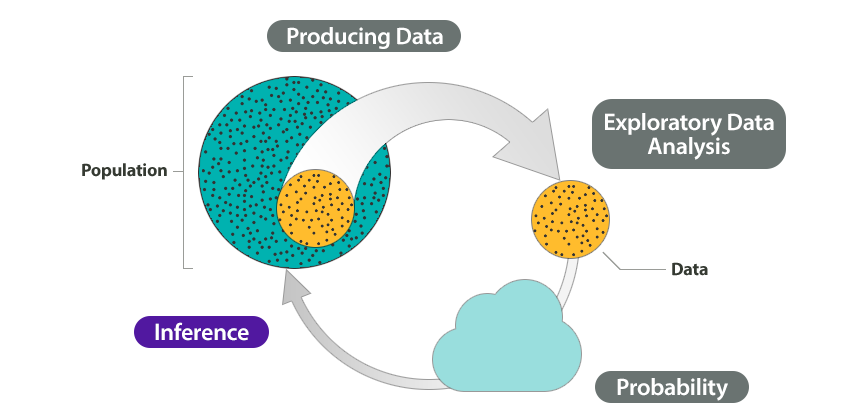
마지막으로 통계적 추론(statistical inference)에 대해 소개하겠습니다. 통계적 추론은 “모집단에 대한 어떤 미지의 양상을 관측치로부터 통계학을 이용하여 추측하는 과정"입니다.

통계적 추론의 도식화

통계적 추론의 도식화

조금 더 엄밀한 설명을 위해 다음의 용어들을 소개하겠습니다.

  • 모수(parameter) $\theta$: 모집단의 성질을 요약하는, 알고자 하는 미지의 값을 의미합니다.
  • 관측치(observation) $x$: 우리가 관측하는 자료로 그 확률분포가 모수에 영향을 받는 확률변수라 가정합니다.

관측치가 모수에 따라 분포가 변한다는 것을 $x|\theta \sim f(x|\theta)$로 표기하기도 합니다. 이는 $f(x|\theta)$를 $x$가 가지고 있는 $\theta$의 정보로 생각할 수 있음을 의미합니다.

예를 들어, 지하의 연구실에서 일하는 A와 B가 있는데 어느날 A가 비에 젖은 우산을 들고왔다고 하겠습니다. 그러면 $B$는 “내가 출근할 때는 맑았었는데 지금은 비가 오나보다"하고 생각할 것입니다. 이러한 추론의 근거는 비가 왔을 때, A가 비에 젖은 우산을 들고왔을 확률이 매우 높고 비가 오지 않았을 때, A가 비에 젖은 우산을 들고왔을 확률이 매우 낮은 데에 있습니다. 이처럼, 통계적 추론은 관측치 $x$를 보고 모수 $\theta$에 대해 추론하는 과정으로 생각할 수 있습니다.

기계학습과의 관계

기계학습(machine learning, 머신러닝)의 지도학습(supervised learning) 문제에서는 설명변수(explanatory variable) $x$와 반응변수 $y$의 관계를 통계적 모형으로 나타내고, 이를 추정해야합니다.

앞서 소개한 일기예보 문제에서, 대기상태(기온, 습도 등) $x$ 가 주어졌을 강수확률을 $f(x)$로 나타내는 모형을 생각하기로 하였습니다. 비가 내리는 사건을 $y = 1$, 비가 내리지 않는 사건을 $y=0$이라 하면, 이 모형은 성공률이 $p$인 베르누이 분포 $Ber(p)$를 사용하여 $$ y | x \sim Ber(f(x)) $$ 와 같이 나타낼 수 있습니다.

이러한 문제는 주어진 훈련자료(train data)로부터 실제 자료(data)의 경향성을 잘 설명하는 모형 $f$를 적합하는(fit) 것이라 할 수 있는데 훈련자료를 관측치, 모형을 모수로 대응시키면 통계적 추론과 같은 구조를 가지고 있음을 확인할 수 있습니다. 때문에, 통계적 추론에서 사용하는 방법들 (최대가능도추정, 회귀계수에 대한 검정, 베이즈 추론 등) 모두는 기계학습에서 그대로 사용됩니다.

지도학습 뿐 아니라, 생성모형(generative model), 군집 모형(clustering)과 같은 일반적인 기계학습 모형에서도 통계적 모형을 사용하고, 모형의 적합 과정에서 통계적 추론이 사용됩니다. 즉, 우리가 알고 있는 기계학습 모형들에 대해서도 베이즈 추론을 적용하여 베이즈 기계학습 모형(Bayesian machine learning model)을 제안할 수 있습니다.

베이즈 추론에 대한 자세한 설명은 다음에 소개하겠습니다.

comments powered by Disqus
CATALOG
    FEATURED TAGS
    bayesian r statistics