\[ \newcommand{\prob}[1]{\mathbb{P}\!\left(#1\right)} \] \[ \newcommand{\expt}[1]{\mathbb{E}\!\left[#1\right]} \] \[ \newcommand{\Cov}[2]{\text{Cov}\!\left(#1,#2 \right)} \] \[ \newcommand{\Var}[1]{\text{Var}\!\left(#1\right)} \] \[ \newcommand{\Natural}{\mathbb{N}} \] \[ \newcommand{\real}{\mathbb{R}} \] \[ \newcommand{\dint}{\displaystyle\int} \] \[ \newcommand{\ind}[1]{I\!\left(#1\right)} \]

1 분산분석

분산 분석(analysis of variance, ANOVA, 변량 분석)은 통계학에서 두 개 이상 다수의 집단을 비교하고자 할 때 집단 내의 분산, 총평균과 각 집단의 평균의 차이에 의해 생긴 집단 간 분산의 비교를 통해 만들어진 F분포를 이용하여 가설검정을 하는 방법이다. 통계학자이자 유전학자인 로날드 피셔(R.A. Fisher)에 의해 1920년대에서 1930년대에 걸쳐 만들어졌다.1

1.1 분산분석의 용어

  • 인자(요인; factor): 관측값에 영향을 주는 속성 (독립변수)
  • 인자 수준(factor lecel): 인자가 취할 수 있는 값들
  • 처리(treatment): 특정 인자를 적용하는 것
  • \(n\)원 배치법(\(n\)-way ANOVA): 인자의 종류가 \(n\)개인 모형 (일원배치법, 이원배치법, etc.)

2 일원배치법

2.1 일원배치법

  • 인자가 한 종류인 분산분석 모형을 일원배치법 모형이라 한다.
  • 처리 \(i\)들에 대해 반응변수를 \(y_{ij}\), 처리의 효과를 \(\alpha_i\)라 하자.
  • 일원배치법의 모형은 다음과 같이 나타낼 수 있다. \[y_{ij} = \mu + \alpha_i + \epsilon_{ij}, \quad j=1,2,\cdots, n_i, \quad \sum_{i=1}^k n_i \alpha_i = 0\]
  • 여기서 \(\mu\)는 총 평균을, \(\epsilon_{ij} \sim N(0, \sigma^2)\)는 오차를 뜻한다.

참고: 일원배치모형을 독립변수가 범주형인 회귀모형으로 생각해볼 수 있다.

2.2 제곱합의 분해

  • 회귀분석에서와 비슷하게, 다음과 같이 제곱합들을 정의하자.
  1. 총 제곱합: \(SST = \displaystyle\sum_{i=1}^k \displaystyle\sum_{j=1}^{n_i} (y_{ij} - \bar{y}_{..})^2, ~\left(df = N-1 = \displaystyle\sum_{i=1}^k n_i - 1\right)\)
  2. 잔차제곱합: \(SSE = \displaystyle\sum_{i=1}^k \displaystyle\sum_{j=1}^{n_i} (y_{ij} - \bar{y}_{i.})^2,~ \left(df = N-k\right)\)
  3. 처리제곱합: \(SS_{tr} = \displaystyle\sum_{i=1}^k \displaystyle\sum_{j=1}^{n_i} (\bar{y}_{i.} - \bar{y}_{..})^2,~ \left(df = k-1 \right)\)
  • 그러면 다음이 성립한다. \[SST = SSE + SS_{tr}\]

2.3 일원배치법의 검정

  • 처리효과의 유의성 검정은 다음의 귀무가설을 검정하는 것으로 생각할 수 있다. \[H_0:~ \alpha_1 = \cdots = \alpha_k = 0, \quad H_1: \text{ not }H_0\]
  • 검정통계량으로는 \(F = \dfrac{MS_{tr}}{MSE}\)를 사용하며 귀무가설 하에서 \(F \sim F(k-1, n-k)\)임을 이용한다.
  • 분산분석의 검정은 이전 시간에 언급했던 ANOVA table 을 이용해 실시한다.

2.4 예제

  • R에는 기본적으로 내장된 데이터들이 있다.
  • 그 중 가장 유명한 것으로 아이리스(붓꽃)의 특성들을 기록한 iris 자료가 있다.
  • iris는 통계학자 Fisher가 소개한 데이터로, 붓꽃의 3가지 종 setosa, versicolor, virginica에 대해 꽃받침(sepal)과 꽃잎(petal)의 길이와 너비를 정리한 것이다.
  • 구체적으로, iris 데이터의 성분은 다음으로 이루어져있다.
열 의미 자료형
Sepal.Length 꽃받침의 길이 숫자형
Sepal.Width 꽃받침의 너비 숫자형
Petal.Length 꽃잎의 길이 숫자형
Petal.Width 꽃잎의 너비 숫자형
Species 붓꽃의 종 범주형
  • 붓꽃의 종에 따라 꽃받침의 길이에 차이가 있는지를 유의수준 5%에서 검정해보자.
  • 일원배치모형을 이용해 다음의 가설을 검정하자.

\[H_0:\alpha_1=\alpha_2=\alpha_3=0, \quad \text{vs} \quad H_1:\text{적어도 한 $\alpha_i$는 0이 아니다.}\]

  • iris 자료에서는 붓꽃의 종이 인자형(factor)으로 저장되어 있으나, 그렇지 않은 자료가 있다면 factor() 함수를 사용해 변환하면 된다.
  • 분산분석은 lm() 함수를 통해 회귀모형을 적합한 뒤, anova() 함수를 이용해 분산분석표를 얻어 실시한다.
  • 일원배치 분산분석은 다음과 같이 실시할 수 있다.
  • 분산분석 결과, 검정통계량의 값은 \(F_0 = 119.26\) 이고 유의확률은 매우 작은 것이다.
  • 따라서 유의수준 5%에서 모평균이 모두 동일하다는 귀무가설을 기각할 수 있다.
  • 즉, 붓꽃의 종에 따라 꽃받침의 길이에 차이가 있다고 할 만한 유의한 증거가 있다고 할 수 있다.

3 이원배치법

  • 인자가 두 종류인 분산분석 모형을 이원배치법 모형이라 한다.
  • 처리 \(i\)들에 대해 반응변수를 \(y_{ijk}\), 처리의 효과들을 각각 \(\alpha_i\), \(\beta_j\)라 하자.
  • 또한, 교호작용(interaction)의 효과 \(\gamma_{ij}\)를 도입하자.
  • 이원배치법의 모형은 다음과 같이 나타낼 수 있다. \[y_{ijk} = \mu + \alpha_i + \beta_j + \gamma_{ij} + \epsilon_{ijk},\] \[i = 1,2,\cdots, p,\quad j=1,2,\cdots,q, \quad k=1,2,\cdots,n_{ij},\] \[\sum_{i=1}^p n_{ij} \alpha_i = \sum_{j=1}^q n_{ij} \beta_j = 0\]
  • 여기서 \(\mu\)는 총 평균을, \(\epsilon_{ijk} \sim N(0, \sigma^2)\)는 오차를 뜻한다.

참고: 이원배치모형 또한 독립변수가 범주형인 회귀모형으로 생각해볼 수 있다.

3.1 제곱합의 분해

  • 일원배치법 모형에서와 비슷하게, 다음과 같이 제곱합들을 정의하자.
  1. 총 제곱합: \(SST = \displaystyle\sum_i \displaystyle\sum_j \displaystyle\sum_k (y_{ijk} - \bar{y}_{...})^2\)
  2. 인자 \(A\)의 제곱합: \(SS_A = \displaystyle\sum_i \displaystyle\sum_j \displaystyle\sum_k (\bar{y}_{i..} - \bar{y}_{...})^2\)
  3. 인자 \(B\)의 제곱합: \(SS_B = \displaystyle\sum_i \displaystyle\sum_j \displaystyle\sum_k (\bar{y}_{.j.} - \bar{y}_{...})^2\)
  4. 교호작용의 제곱합: \(SS_{A\times B} = \displaystyle\sum_i \displaystyle\sum_j \displaystyle\sum_k (\bar{y}_{ij.} - \bar{y}_{i..}-\bar{y}_{.j.}+ \bar{y}_{...})^2\)
  5. 잔차제곱합: \(SSE = \displaystyle\sum_i \displaystyle\sum_j \displaystyle\sum_k (y_{ijk} - \bar{y}_{ij.})^2\)
  • 그러면 다음이 성립한다. \[SST = SSE + SS_A + SS_B + SS_{A\times B}\]

3.2 이원배치법의 검정

  • 처리효과의 유의성 검정은 다음의 귀무가설들을 검정하는 것으로 생각할 수 있다. \[H_0:~ \alpha_1 = \cdots = \alpha_p = 0, \quad H_1: \text{ not }H_0\] \[H_0:~ \beta_1 = \cdots = \beta_q = 0, \quad H_1: \text{ not }H_0\] \[H_0:~ \gamma_{11} = \cdots = \gamma_{pq} = 0, \quad H_1: \text{ not }H_0\]
  • 검정통계량으로는 \(F = MS_{x}/MSE\) 를 사용하며 귀무가설 하에서 \(F \sim F(df_{x}, N - pq)\)임을 이용한다.
  • 분산분석의 검정은 ANOVA table 을 이용해 실시한다.

3.3 예제

  • 다음은 새로운 해열제의 효과를 확인하기 위한 실험의 결과이다.
  • 인자 medi는 해열제의 처방 여부 (0: 처방하지 않음, 1: 해열제, 2: placebo), 인자 gender는 피실험자의 성별, 변수 temp는 환자의 체온 변화를 의미한다.
  • 해열제의 효과를 \(\alpha\), 성별의 효과를 \(\beta\), 교호작용을 \(\gamma\)라 하자.
  • 해열제의 처방과 성별에 따라 체온 변화에 차이가 있는지를 유의수준 5%에서 검정해보자.
  • 이원배치모형을 이용해 다음의 가설을 검정하자.

\[H_0:~ \alpha_1 = \alpha_2 = \alpha_3 = 0, \quad H_1: \text{ not }H_0\] \[H_0:~ \beta_1 = \beta_2 = 0, \quad H_1: \text{ not }H_0\] \[H_0:~ \forall \gamma_{ij} = 0, \quad H_1: \text{ not }H_0\]

  • 먼저 해열제와 성별의 교호작용의 유무를 교호작용 그림(interaction plot)을 통해 확인해보자.
  • R에서는 interaction.plot() 함수를 사용해 그릴 수 있다.

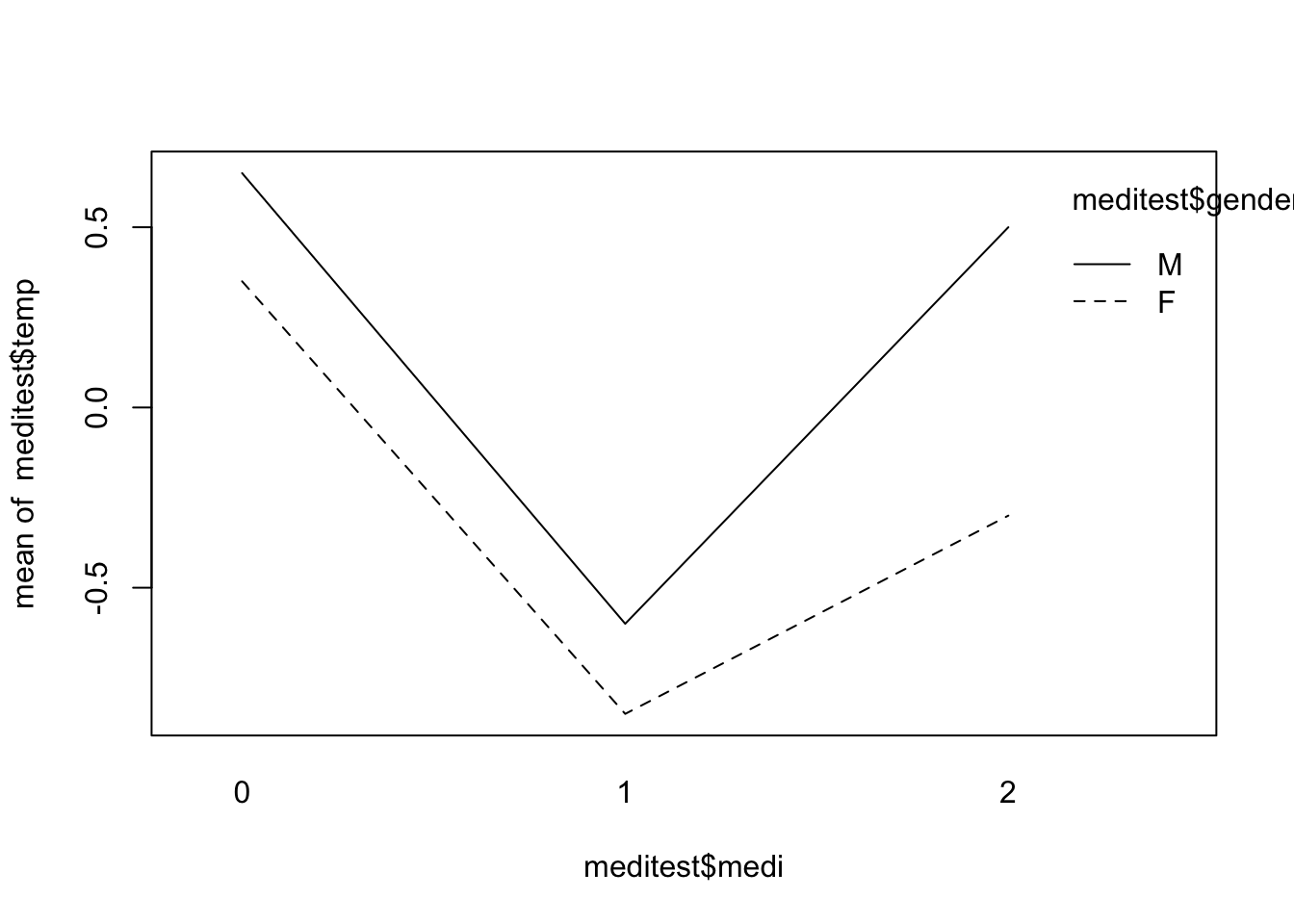
  • 그림의 패턴에 큰 차이가 없는 것으로 보아, 두 요인 사이에는 상호작용이 존재하지 않는 것으로 보인다.
  • 선형회귀모형에서 교호작용은 두 요인을 곱(*)으로 표현하여 다음과 같이 선언할 수 있다.
## 
## Call:
## lm(formula = temp ~ medi * gender, data = meditest)
## 
## Coefficients:
##   (Intercept)          medi1          medi2        genderM  medi1:genderM  
##          0.35          -1.20          -0.65           0.30          -0.05  
## medi2:genderM  
##          0.50
  • 분산분석 결과는 다음과 같이 확인할 수 있다.

  • 분산분석 결과, 해열제는 효과가 있으나 성별, 해열제와 성별의 교호작용은 모두 확인할 수 없었다.

  • 또는, 다음과 같이 교호작용을 제외한 상태로 분산분석을 진행할 수도 있다.

  • 앞에서와 비슷한 결론을 내릴 수 있다.

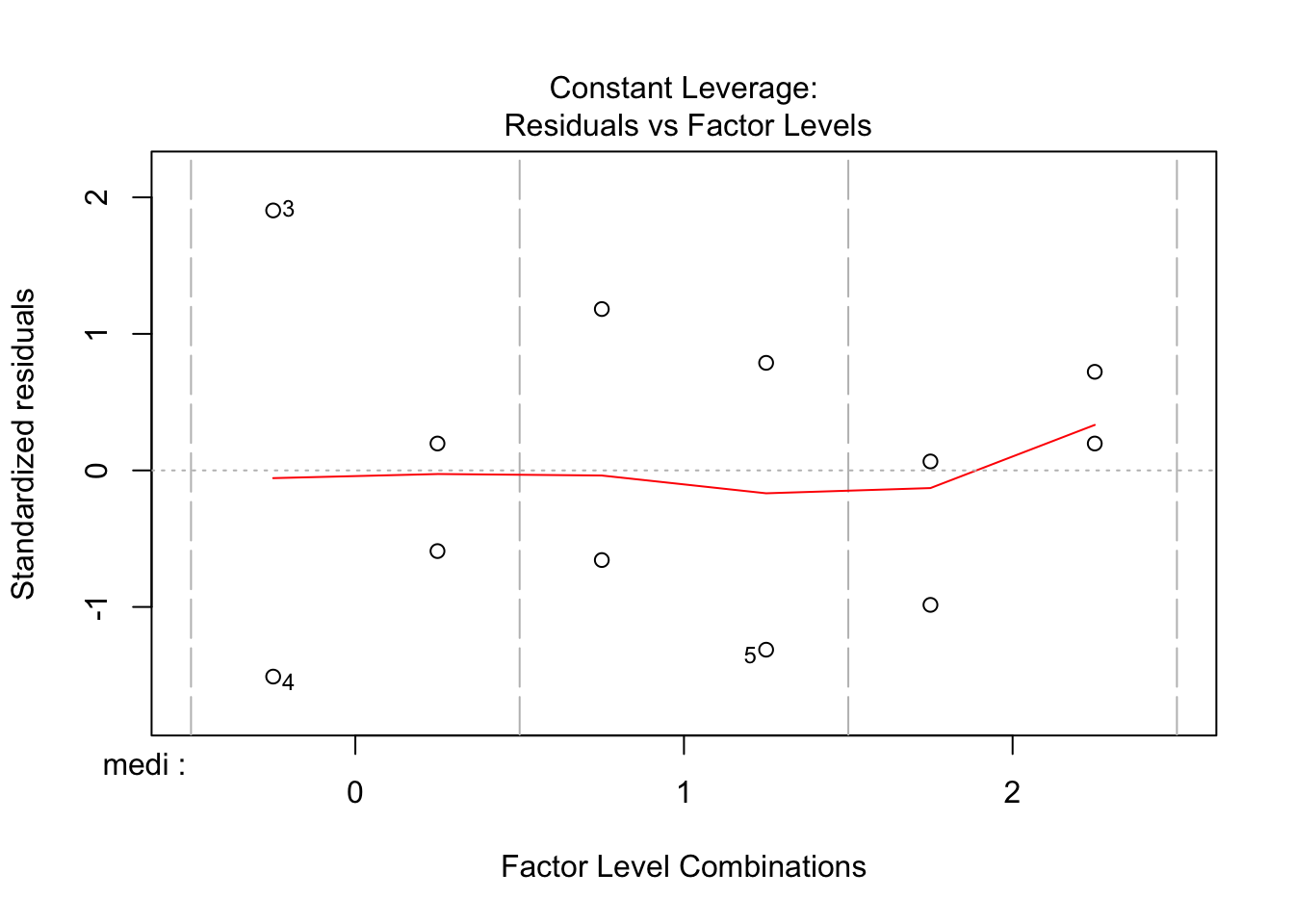
  • 참고로, 분산분석에서도 회귀분석과 마찬가지로 오차항에 대한 정규성 가정을 사용하기 때문에, 잔차분석을 통해 정규성 검정을 진행하기도 한다.

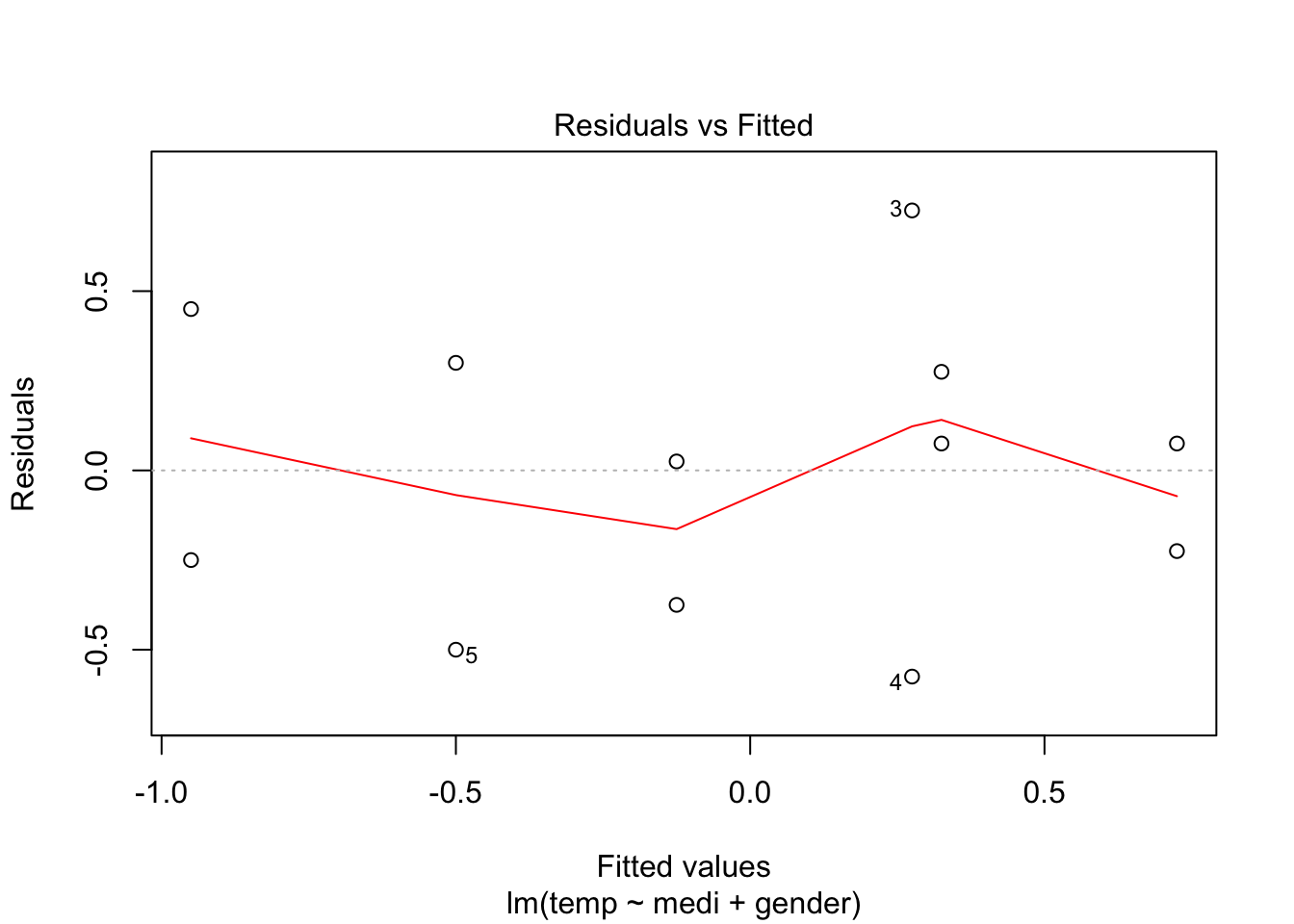
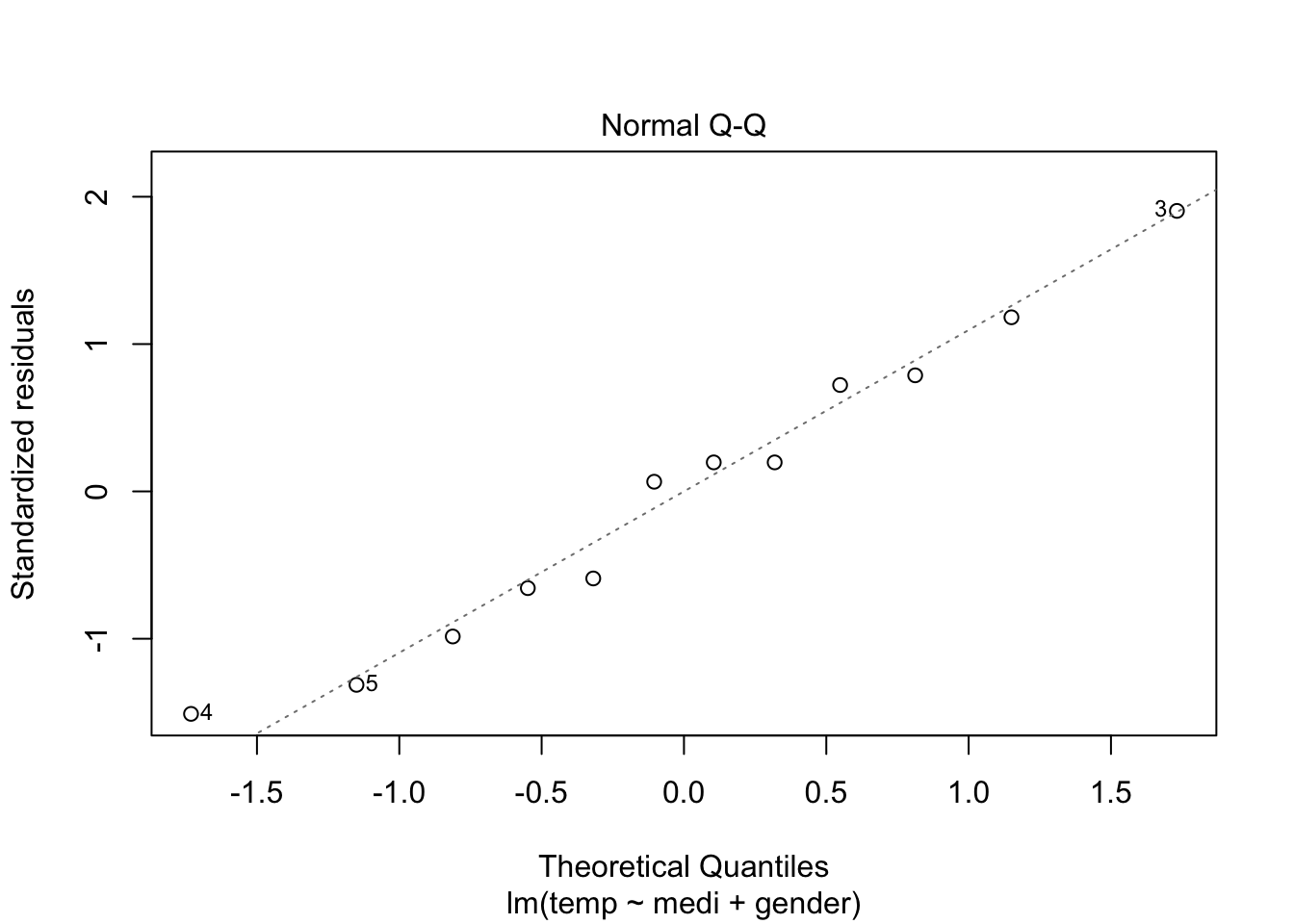
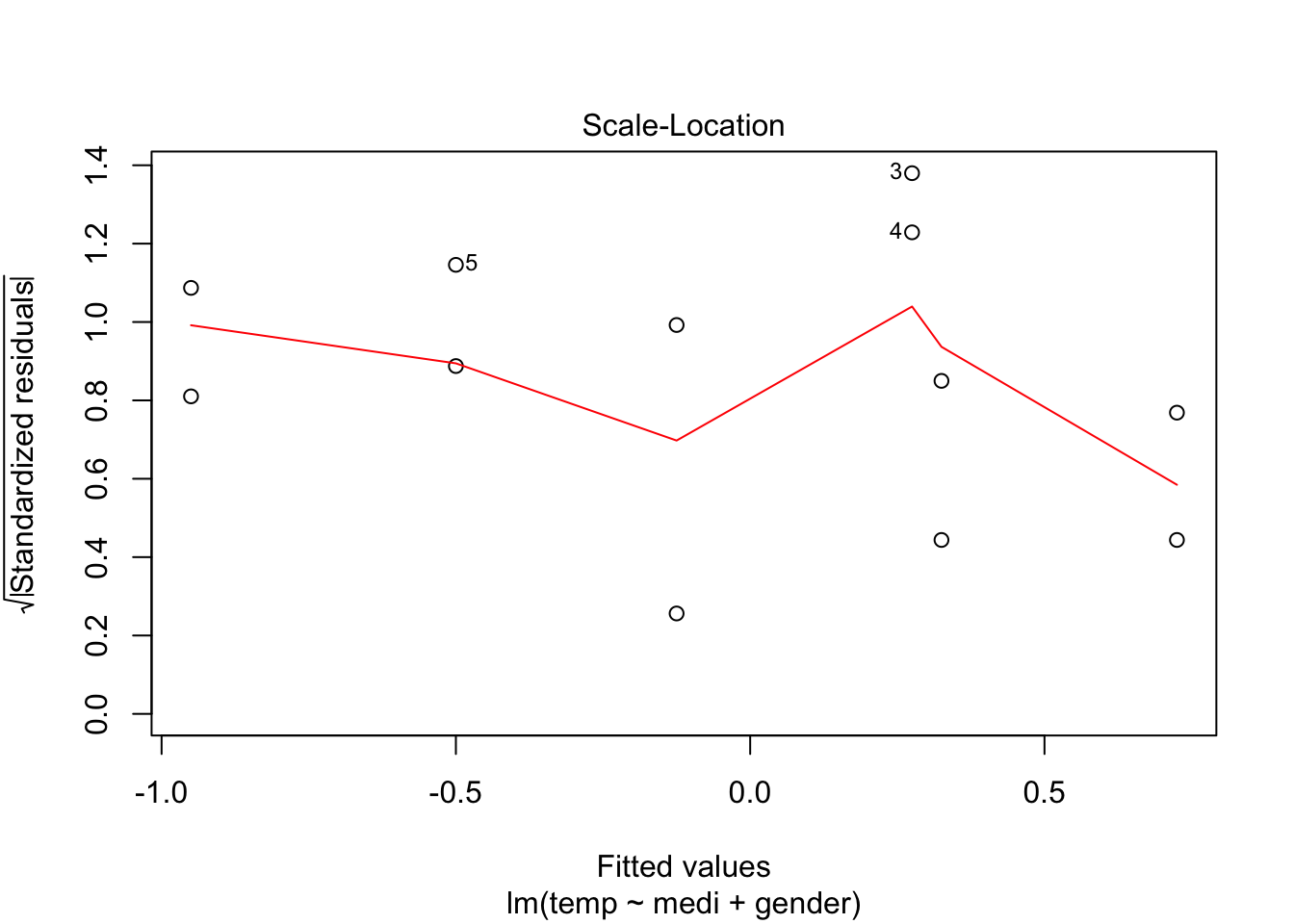
4 실습

4.1 목표

오래 나는 종이비행기를 만들어보자!

  • 다음 링크에는 여러가지 종이비행기를 접는 방법들이 소개되어있다.
  • 오래 나는 종이비행기는 어떤 비행기일지 실험을 직접 설계하여 알아보자.

4.2 실험계획법

4.2.1 실험 방법

  1. 조별로 각자 6종류의 종이비행기를 만든다. Glinder1, Glinder2, Delta인 경우, 그리고 종이가 A4, 시험지인 경우를 생각한다. <> 종이비행기를 접는 방법은 임의로 변경하지 않도록 한다.
  2. 각 비행기를 5번씩 날리고, 비행 시간을 기록한다. <> 종이비행기를 날리는 사람은 한 사람으로 통일한다.

4.2.2 주의

  1. 환경의 변동(natural variation)으로 인한 차이가 존재하는가? (예: 종이비행기를 날리는 사람의 키차이로 인해 비행시간의 차이가 나타났다). 그룹 간 실제 변동(group variability)과 측정오차(measurement error)를 구분하자.
  2. 같은 조건의 종이비행기들은 비행시간이 얼마나 차이가 나는가? (1조와 3조의 A4 Glinder1)
  3. 비행시간의 유의미한 차이를 보기 위해선 비행기나 종이의 종류가 어떻게 달라져야 하는가?

4.3 실험

  • 조별로 실험을 실시한 뒤, 결과를 다음과 같이 anova_df_n (n: 조) 에 정리하자.

4.4 분석

4.4.1 가정

본 실험에서는 다음의 가정들이 적절하게 만족되었다고 생각하고 분석을 진행한다.

  1. 독립성(Independence): 모든 비행은 각각 독립이어야 한다.
  2. 정규성(Approximately normal): 각 그룹 내의 비행시간은 정규분포를 따라야 한다.
  3. 등분산성(Constant variance): 각 그룹 내의 비행시간의 분산은 그룹끼리 비교했을 시 큰 차이가 없어야 한다.

4.4.2 자료

  • 수집한 자료에 대해 분산분석을 시행해보자.
  • 가령, 다음과 같이 자료가 얻어졌다고 하자.

검정하고자 하는 가설은 다음과 같다. (단, \(\alpha_i\)는 비행기의 종류에 따른 효과이고, \(\beta_j\)는 종이의 종류에 따른 효과이고 \(\gamma_ij\)는 비행기의 종류와 종이 종류의 교호작용을 의미한다.)

\[\begin{align*} &H_0: \alpha_1 = \alpha_2 = \alpha_3 = 0\\ &H_0: \beta_1 = \beta_2 = 0\\ &H_0: \gamma_{ij} = 0 \quad \forall i,j \end{align*}\]

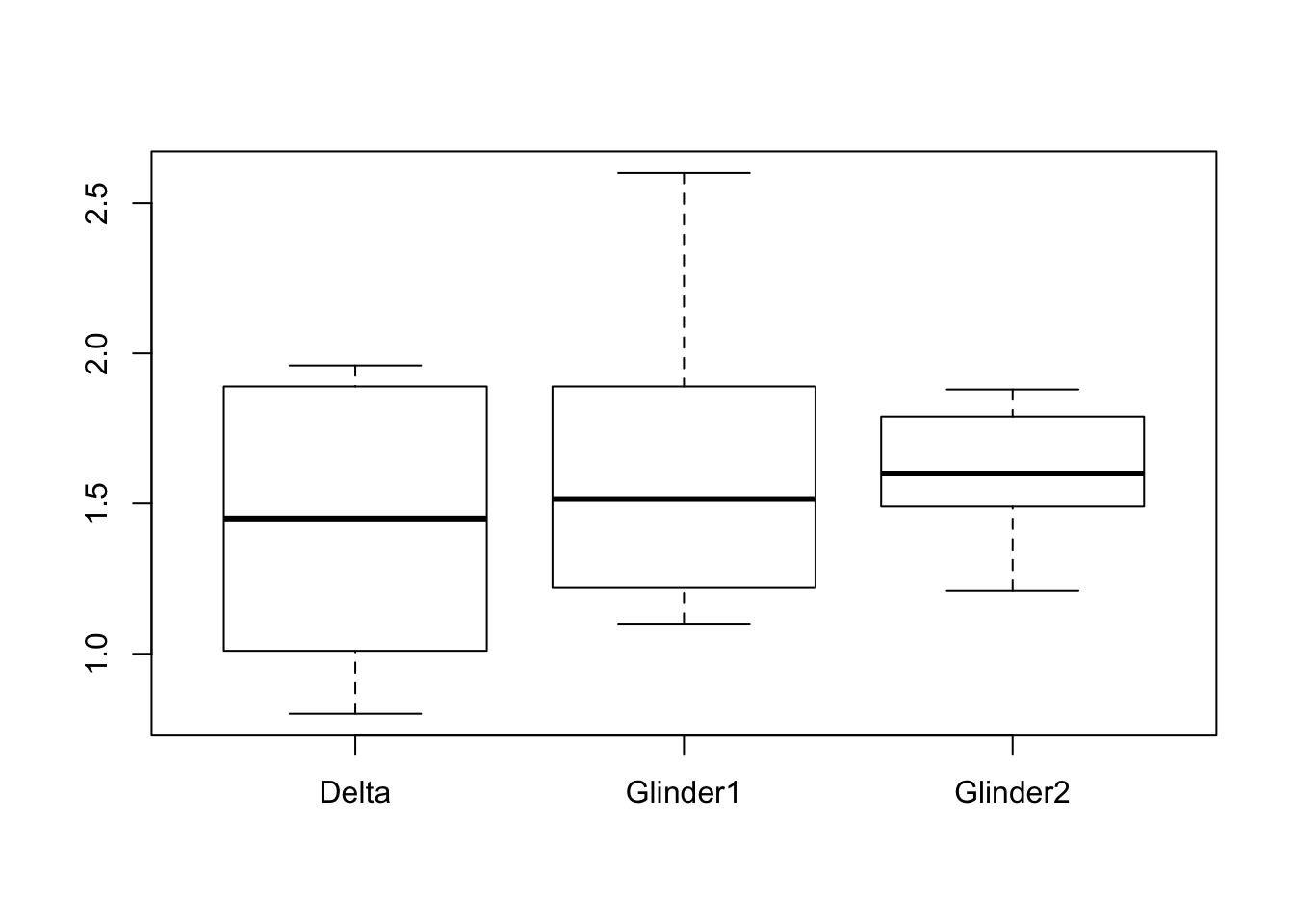
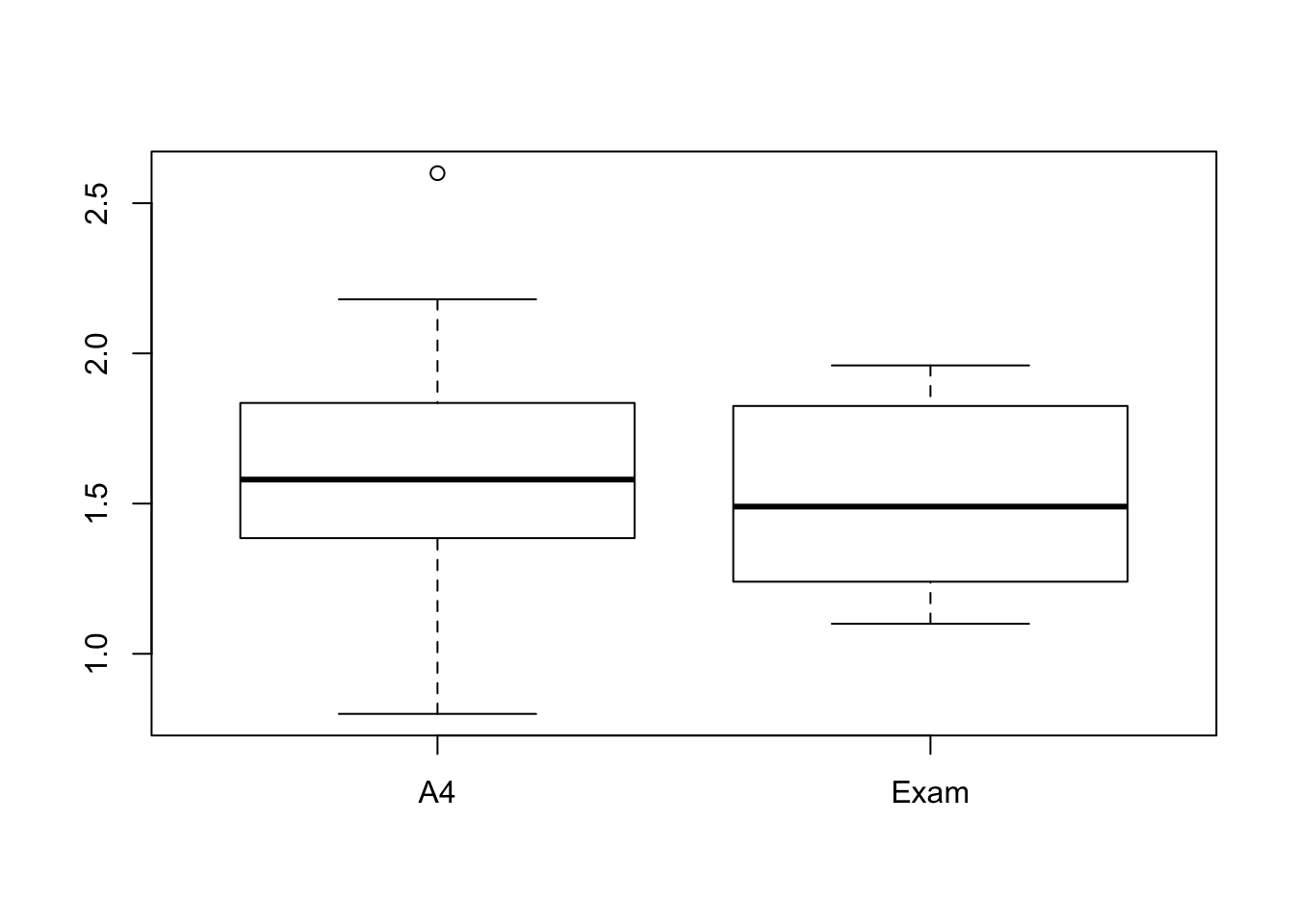
4.4.3 box-plot

  • 비행기의 종류와 종이 종류에 따른 비행시간의 차이가 있는지를 simple box-plot과 side-by-side boxplot를 통해 확인해보자.

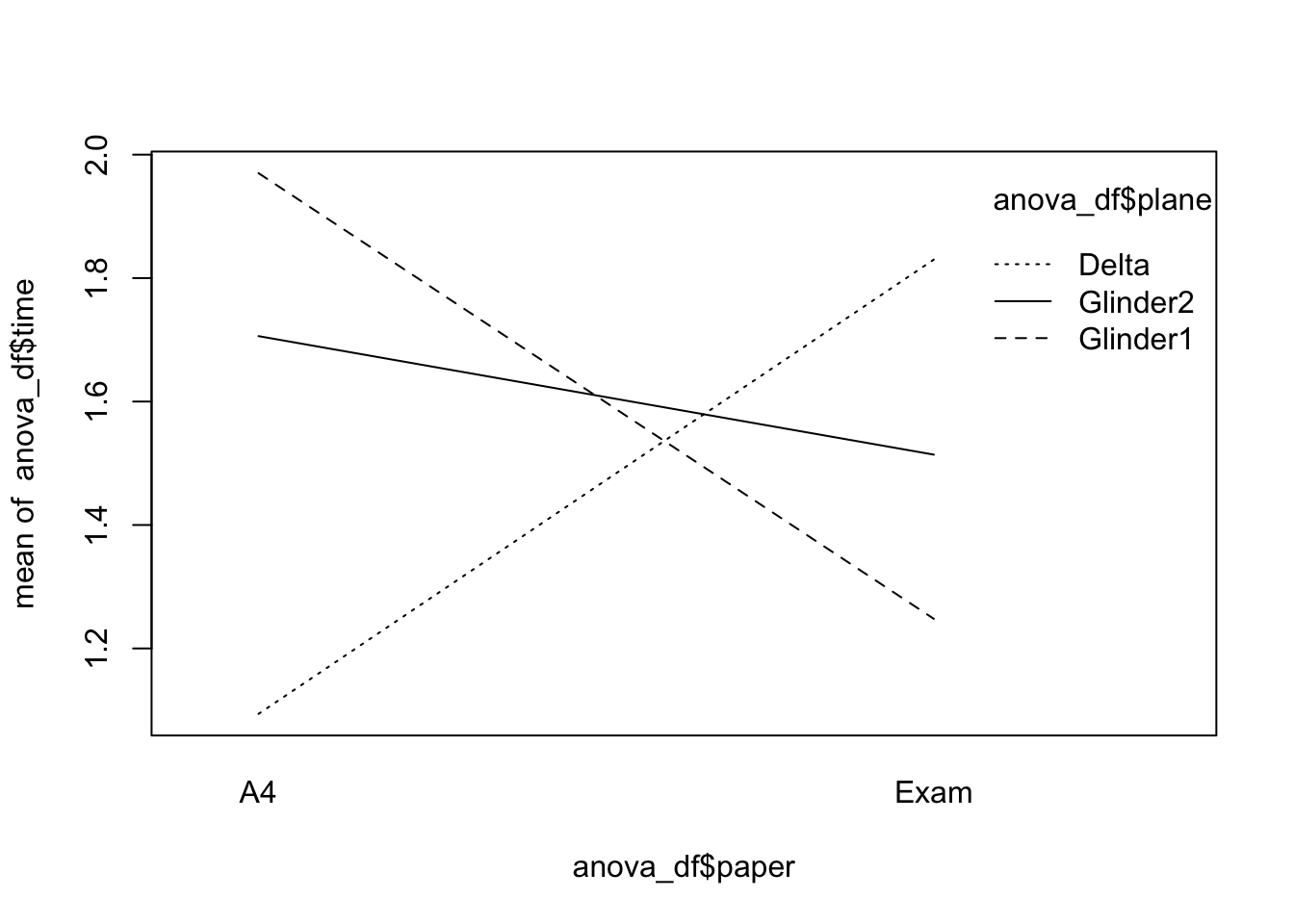
4.4.4 interaction plot

  • 비행기 종류와 종이 종류에 대한 상호작용의 유무를 평균그림을 통해 확인해보자.

4.4.5 ANOVA

  • 다음과 같이 분산분석을 실시하자.

과제

마지막 과제는 채점되지 않습니다. 또한 제출하지 않으셔도 별다른 패널티는 존재하지 않습니다. 단, 문제를 풀다 어려운 점이 있으시면 언제든지 조교에게 메일을 통해 물어보시면 됩니다.

Problem 1

  • 각 조의 자료를 이용해 다음 질문에 답하여라.
  1. 비행기의 종류가 비행시간에 영향을 미치는 지를 일원배치법을 통해 알아보아라.
  2. 비행기의 종류와 종이 종류의 교호작용을 고려하지 않고 이원배치법을 통해 이들이 비행시간에 영향을 미치는지를 알아보아라.
  3. 비행시간의 정규성 가정을 qqplot 을 그려 확인해보아라.

  1. Wikipedia 분산분석, Link↩