상관분석과 회귀분석
2018 가을학기 통계학실험 010 강좌
이경원
November 27, 2018
1 상관분석
- 상관분석(correlation analysis)란 두 변수 사이의 선형적 연관성에 관한 추론을 뜻한다.
1.1 상관계수
- 두 확률변수 \(X\), \(Y\)의 모상관계수(population correlation coefficient)는 다음과 같이 정의된다. \[\rho = corr(X, Y) = \frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}\]
- 상관계수의 절댓값 \(|\rho|\)가 1에 가까울수록 두 변수는 강한 상관관계가 있다고 말할 수 있고, 0에 가까울수록 약한 상관관계를 갖는다 말할 수 있다.
- 또한, 상관계수는 -1과 1 사이의 값만을 가질 수 있다.
- \((X,Y)\)의 표본을 \((x_1,~y_1),~\cdots, (x_n,y_n)\)이라 할 때, 모상관계수의 추정량으로 다음의 표본상관계수(sample correlation coefficient) \(r\)을 사용할 수 있다. \[r = \frac{\sum_{i=1}^n(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i -\bar{x})^2 \sum_{i=1}^n (y_i - \bar{y})^2}}\]
- 표본상관계수 또한 \(-1 \leq r \leq 1\)을 만족한다. (Cauchy-Schwarz’s inequality])
- R에서 표본상관계수는
cor()함수를 사용해 계산할 수 있다.
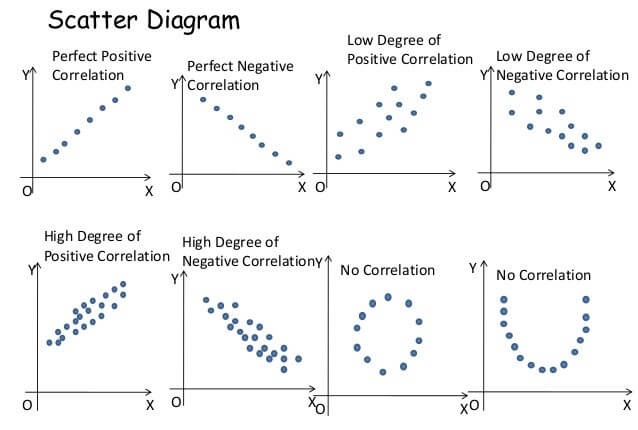
Scatter Diagram, copyright on myassignmenthelp.net
1.2 상관관계에 대한 검정
- 두 변수 \(X\)와 \(Y\)에 상관관계가 존재하는지 아닌지에 대한 검정은 다음의 귀무가설을 검정하는 것을 뜻한다. \[H_0: \rho = 0.\]
- 검정통계량으로는 표본상관계수 \(r\)을 이용한 \(T = \sqrt{n-2} \dfrac{r}{\sqrt{1-r^2}}\)을 사용하며 귀무가설 하에서 \(T \sim t(n-2)\)임이 알려져 있다.
- 따라서, 유의수준 \(\alpha\)에서 기각역은 다음과 같이 주어진다.
| 가설 | 기각역 | 유의확률 |
|---|---|---|
| \(H_1\): \(\rho\) > 0 | \(T \geq t_{\alpha}(n-2)\) | \(\mathbb{P}(T \geq t_0)\) |
| \(H_1\): \(\rho\) < 0 | \(T \leq t_{\alpha}(n-2)\) | \(\mathbb{P}(T \leq t_0)\) |
| \(H_1\): \(\rho \neq 0\) | \(|T| \geq t_{\alpha/2}(n-2)\) | \(\mathbb{P}(|T| \geq |t_0|)=2 \mathbb{P}(T \geq |t_0|)\) |
- R에서 상관관계에 대한 검정은
cor.test()함수를 사용해서 실시할 수 있다.
1.3 실습
- 미세먼지는 지름이 10\(\mu\)m(마이크로미터, 1\(\mu\)m=1000분의 1㎜) 이하의 먼지로 PM(Particulate Matter)10이라고 한다.
- 자동차 배출가스나 공장 굴뚝 등을 통해 주로 배출되며 중국의 황사나 심한 스모그때 날아오는 크기가 작은 먼지를 말한다.
- 미세먼지중 입자의 크기가 더 작은 미세먼지를 초미세먼지라 부르며 지름 2.5\(\mu\)m 이하의 먼지로서 PM2.5라고 한다.
pmkw.Rdata에는 2017년도 상반기 관악구의 미세먼지농도가 기록되어있다.- 다음의 링크를 통해 자료를 다운로드 받은 뒤, 다음 명령어를 통해 실습을 위한 자료를 불러오자.
- 초미세먼지 농도
PM25변수와 미세먼지 농도PM10변수의 관련성에 대해 알아보자. - 먼저, 두 변수에 대한 산점도를 그려보면 다음과 같다.
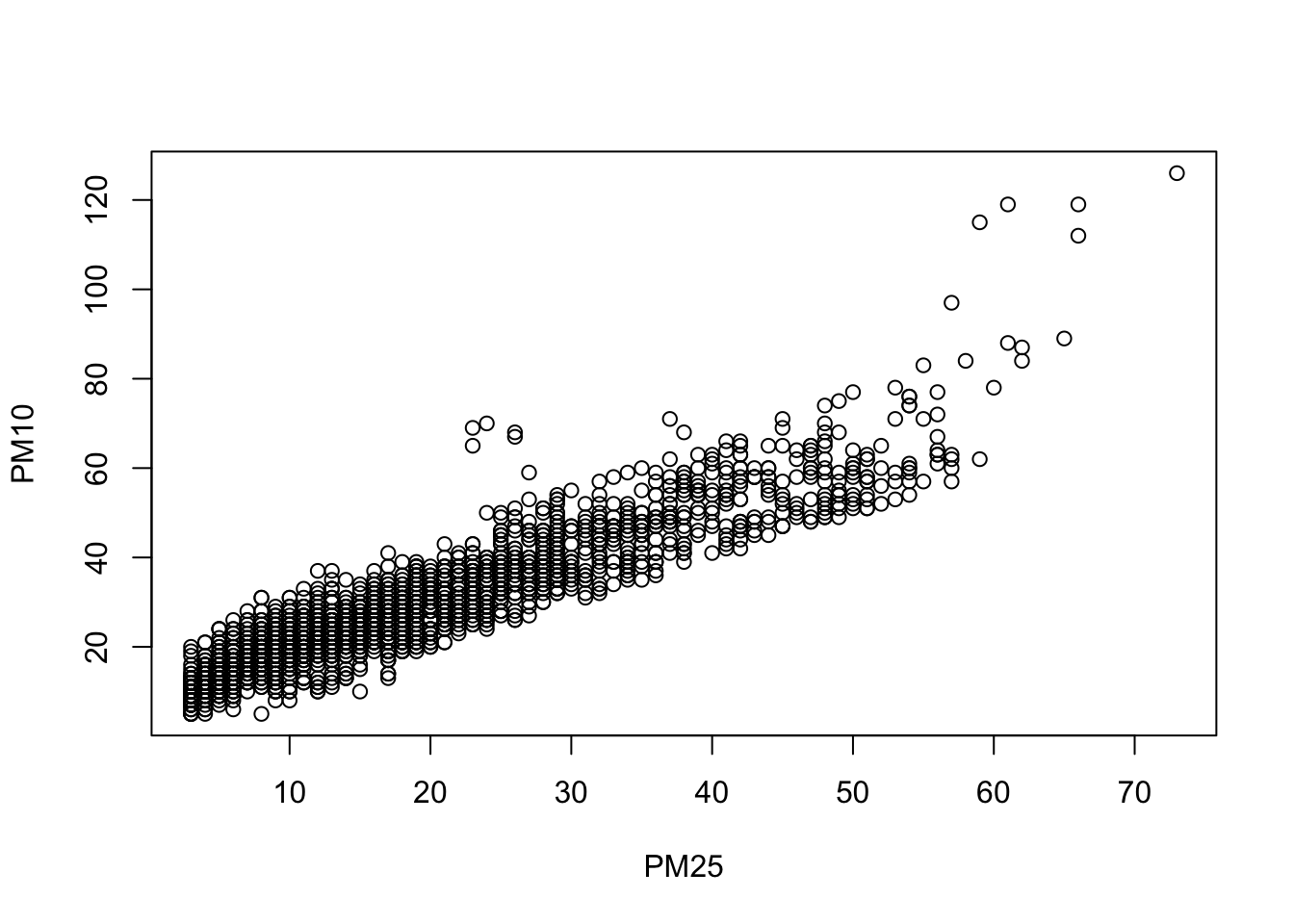
- 그래프 상에서도 두 변수 사이에는 강한 양의 상관관계가 존재한다는 것을 알 수 있고, 실제 상관계수를 계산해보면 0.92 로 높은 값이 계산된다.
- 상관관계의 유무에 대한 검정을 유의수준 5%에서 실시해보자.
##
## Pearson's product-moment correlation
##
## data: pmkw$PM10 and pmkw$PM25
## t = 100, df = 2000, p-value <2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.92 0.93
## sample estimates:
## cor
## 0.92- 검정 결과 유의확률이 매우 작은 것으로 확인되었으며 유의수준 5%에서 귀무가설을 기각할 수 있다.
- 즉, 초미세먼지농도와 미세먼지농도 사이에는 상관관계가 존재한다는 매우 뚜렷한 증거가 있다고 말할 수 있다.
- 단측검정을 실시하려면, (즉, 양/음의 상관관계가 존재하는지에 대한 여부가 궁금하다면) 다음과 같이 검정을 실시할 수 있다.
##
## Pearson's product-moment correlation
##
## data: pmkw$PM10 and pmkw$PM25
## t = 100, df = 2000, p-value <2e-16
## alternative hypothesis: true correlation is greater than 0
## 95 percent confidence interval:
## 0.92 1.00
## sample estimates:
## cor
## 0.92##
## Pearson's product-moment correlation
##
## data: pmkw$PM10 and pmkw$PM25
## t = 100, df = 2000, p-value = 1
## alternative hypothesis: true correlation is less than 0
## 95 percent confidence interval:
## -1.00 0.93
## sample estimates:
## cor
## 0.922 회귀분석
- 두 변수 \(x\), \(y\)에 대하여 \(y = f(x)\)의 함수관계가 있을 때, \(x\)를 설명변수(explanatory variable) 또는 독립변수(independent variable)이라 부르고, \(y\)를 반응변수(response variable) 또는 종속변수(dependent variable)이라 한다.
- 회귀모형이란 반응변수(일반적으로 연속형)와 설명변수 사이의 함수관계를 가정한 통계적 모형을 뜻한다.
- 이떄 설명변수 \(x\)가 1개일 때(일차원일 때) 이 모형을 단순회귀모형(simple regression), 그 이상일 때를 중회귀모형(multiple regression)이라 하고 함수 \(f(x)\)가 직선(혹은 평면)일 때, 이 모형을 선형회귀모형(linear regression)이라 한다.
- 회귀분석이란 주어진 자료로부터 회귀모형을 찾는 분석과정을 뜻한다.
Galton’s correlation diagram 1886, copyright on wikipedia
2.1 단순선형회귀분석
2.1.1 단순선형회귀모형
- 단순선형회귀모형은 두 변수 \(x\), \(y\)의 관측치 \((x_1,~y_1),~\cdots, (x_n,y_n)\)의 관계를 다음과 같이 나타낸 모형을 의미한다. \[ y_i = \beta_0 + \beta_1 x_i + \epsilon_i\]
- 여기서 회귀계수 \(\beta_0\)는 상수항(절편), \(\beta_1\)은 기울기를 나타내며 오차항 \(\epsilon_i\)들은 서로 독립인 정규분포 \(N(0, \sigma^2)\)을 따른다는 것으로 가정한다.
- \(y = \beta_0 + \beta_1 x\)를 모휘귀직선(population regression line), 추정된 모수를 이용한 \(\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x\)를 적합된 회귀직선(fitted regression line), 자료로부터 관측한 오차항의 추정값 \(e_i = y_i - \hat{y_i}\)를 잔차(residual)이라 한다.
2.1.2 단순선형회귀모형의 추정(적합)
- 단순선형회귀모형의 추정은 잔차제곱합 \[\sum_{i=1}^n e_i^2 = \sum_{i=1}^n (y_i - \hat{y}_i)^2 = \sum_{i=1}^n (y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i)^2\]을 최소화하는 \(\hat{\beta}_0\), \(\hat{\beta}_1\)을 찾는 최소제곱법(least squares method)를 사용한다.
- 최소제곱법으로 추정된 회귀계수 \(\hat{\beta}_0\), \(\hat{\beta}_1\)을 최소제곱추정량(least squares estimator)라 한다.
- 간단한 계산을 이용하면 최소제곱추정량들이 다음과 같이 주어진다는 것을 알 수 있다. \[\hat{\beta}_1 = \frac{S_{xy}}{S_{xx}}, \quad \hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x}.\]
- 여기서 \(\bar{a}\)는 관측치의 표본평균, \(S_{ab} = \displaystyle\sum_{i=1}^n (a_i - \bar{a})(b_i - \bar{b})\)를 뜻한다.
2.1.3 회귀계수의 해석
- \(\hat{\beta}_1\) 는 \(x\)가 한 단위 증가할 때, \(y\)가 평균적으로 \(\hat{\beta}_1\) 단위 증가한다는 것을 뜻한다.
- \(\hat{\beta}_1\)가 양수이면 \(x\)가 증가함에 따라 \(y\)는 증가하고, \(\hat{\beta}_1\)가 음수이면 \(x\)가 증가함에 따라 \(y\)는 감소하는 경향성을 보임을 뜻한다.
2.1.4 제곱합의 분해
- \(SST = \displaystyle\sum_{i=1}^n (y_i - \bar{y})^2\)를 자료의 총제곱합이라 한다. 총제곱합(total sum of squares)은 반응변수 \(y\)의 전체 변동을 뜻한다.
- \(SSE = \displaystyle\sum_{i=1}^n (y_i - \hat{y}_i)^2\)를 잔차제곱합(error sum of squares)이라 한다.
- \(SSR = \displaystyle\sum_{i=1}^n (\hat{y}_i - \bar{y})^2\)를 회귀제곱합(sum of squares due to regression)이라 한다.
- 그러면, \(SST = SSE + SSR\)이 성립한다.
- 결정계수(coefficient of determination) \(R^2 = \dfrac{SSR}{SST} = 1-\dfrac{SSE}{SST}\)는 자료의 전체 변동 중 회귀직선이 설명하는 변동의 비율을 뜻한다.
- 결정계수 \(R^2\)에 대해 \(0 \leq R^2 \leq 1\)이 성립하며 결정계수가 1에 가까울수록 회귀직선이 자료를 잘 설명한다는 것을 의미한다.
- \(MSR = SSR/1\), \(MSE = SSR/(n-2)\)을 각각 회귀제곱평균, 잔차제곱평균이라 부르며 오차항 \(\epsilon\)의 분산 \(\sigma^2\)의 추정량으로는 \(MSE\)를 사용한다.
2.1.5 회귀직선의 유의성 검정
- 적합한 회귀직선이 유의한지 아닌지에 대한 검정은 다음의 귀무가설에 대한 검정으로 실시한다. \[H_0: \beta_1 = 0\quad \text{vs} \quad H_1: \beta_1 \neq 0\]
- 오차항 \(\epsilon\)의 분산 \(\sigma^2\)에 대하여 귀무가설 하에서 \[MSR/\sigma^2 \sim \chi^2(1),~MSE/\sigma^2 \sim \chi^2(n-2)\]임이 알려져있다.
- 따라서, 회귀직선의 유의성 검정은 \(F = \dfrac{MSR}{MSE}\)를 사용하며, 검정통계량 \(F\)는 귀무가설 하에서 \(F(1, n-2)\)를 따름을 이용하여 검정을 실시한다.
- 검정통계량 \(F\)를 이용하는 검정은 분산분석표(ANalysis Of VAriance table; ANOVA table)를 작성하여 실시한다.
ANOVA Table, copyright on math.tutorvista.com
2.1.6 회귀계수 \(\beta_1\)에 대한 추론
- 회귀계수 \(\beta_1\)에 대한 추론은 적합된 회귀계수 \(\hat{\beta}_1\)을 이용하여 이루어진다.
- \(\dfrac{\hat{\beta}_1 - \beta_1}{\sqrt{MSE/S_{xx}}} \sim t(n-2)\)임을 이용하면 \(\beta_1\)에 대한 \(100(1-\alpha)\)% 신뢰구간, \(H_0: \beta_1 = \beta_{10}\)에 대한 검정 등을 실시할 수 있다.
2.1.7 평균반응값에 대한 추론
주어진 \(x\)에 대하여 평균반응값 \(\mathbb{E}[y] = \beta_0 + \beta_1 x\)에 대한 추정은 다음과 같이 실시한다.
- 예측값: \(\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x\),
- 표준오차: \(SE(\hat{y}) = \sqrt{MSE \left( \dfrac{1}{n} + \dfrac{(x-\bar{x})^2}{S_{xx}} \right)}\)
신뢰구간: \(\hat{\beta}_0 + \hat{\beta}_1 x \pm t_{\alpha/2}(n-2)SE(\hat{y})\)
2.1.8 실습
2.1.8.1 적합
- 앞서 초미세먼지 농도와 미세먼지 농도 사이에 유의한 상관관계가 존재한다는 것을 확인했다.
- 이번에는 두 변수 사이의 단순선형회귀모형을 적합해보자.
- R에서 회귀모형의 적합은
lm()함수를 사용하면 된다. - 반응변수를
y, 독립변수를x라 했다면,lm(y ~ x)를 실행하면 된다. - data frame을 사용했다면
lm(y ~ x, data = D)와 같이 코드를 작성하면 된다.
##
## Call:
## lm(formula = PM10 ~ PM25, data = pmkw)
##
## Coefficients:
## (Intercept) PM25
## 8.69 1.08- 다음과 같이 회귀모형을 저장하거나 회귀계수를 선택할 수도 있다.
- 적합된 회귀모형은 \(\hat{y} = 8.69 + 1.08x\) 이다.
2.1.8.2 결과 확인
- 회귀모형에 대한 결과를 확인하려면
summary()함수를 사용하면 된다.
##
## Call:
## lm(formula = PM10 ~ PM25, data = pmkw)
##
## Residuals:
## Min 1Q Median 3Q Max
## -14.93 -3.76 -0.19 3.23 44.25
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 8.6884 0.2388 36.4 <2e-16 ***
## PM25 1.0829 0.0102 105.9 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6 on 1977 degrees of freedom
## Multiple R-squared: 0.85, Adjusted R-squared: 0.85
## F-statistic: 1.12e+04 on 1 and 1977 DF, p-value: <2e-16summary()함수에서Call부분은 적합된 모형의 formula 를 보여준다.Residuals는 잔차에 대한 수치적 요약을 보여준다.Coefficients는 회귀계수에 대한 검정결과들을 보여준다. 회귀계수의 유의성 검정에서 \(\beta_1\)에 대한 유의확률이 매우 작으므로, 유의수준 5%에서 이 회귀직선은 유의하다 말할 수 있다.- 결정계수 \(R^2\) 값은 0.85 로 1에 가까운 값이 계산되었으며, 적합한 회귀모형이 전체 자료의 변동 중 85.02%를 설명한다는 것을 뜻한다.
2.1.8.3 분산분석
- 적합된 회귀모형의 분산분석표를 출력하기 위해서는
anova()함수를 사용하면 된다. - 분산분석표에서의 값들은
summary()함수를 사용했을 때의 결과와 동일하다는 것을 알 수 있다.
2.2 잔차분석
2.2.1 잔차분석
- 앞서 선형회귀모형을 적합할 때, 오차항 \(\epsilon\)의 분포에 다음과 같은 성질들을 가정하였다.
- 선형성: \(\mathbb{E}[\epsilon] = 0\), 즉, \(\mathbb{E}[y] = \beta_0 + \beta_1 x\)
- 정규성: \(\epsilon_i \sim N(\cdot, \cdot)\)
- 등분산성: \(Var(\epsilon_i) = \sigma^2\)
- 독립성: \(\epsilon_i\)들은 서로 독립
- 잔차분석(residual analysis)는 잔차를 이용하여 모형/오차항의 가정에 대해 검토하는 과정을 의미한다.
보통 다음과 같은 것들을 확인한다.
선형성: 잔차가 0을 중심으로 분포되어있다.
## ── Attaching packages ────────────────────────────────────────────────────────────────────────────────────────────────────────────── tidyverse 1.2.1 ──## ✔ ggplot2 3.0.0 ✔ purrr 0.2.5
## ✔ tibble 1.4.2 ✔ dplyr 0.7.6
## ✔ tidyr 0.8.1 ✔ stringr 1.3.1
## ✔ readr 1.1.1 ✔ forcats 0.3.0## ── Conflicts ───────────────────────────────────────────────────────────────────────────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()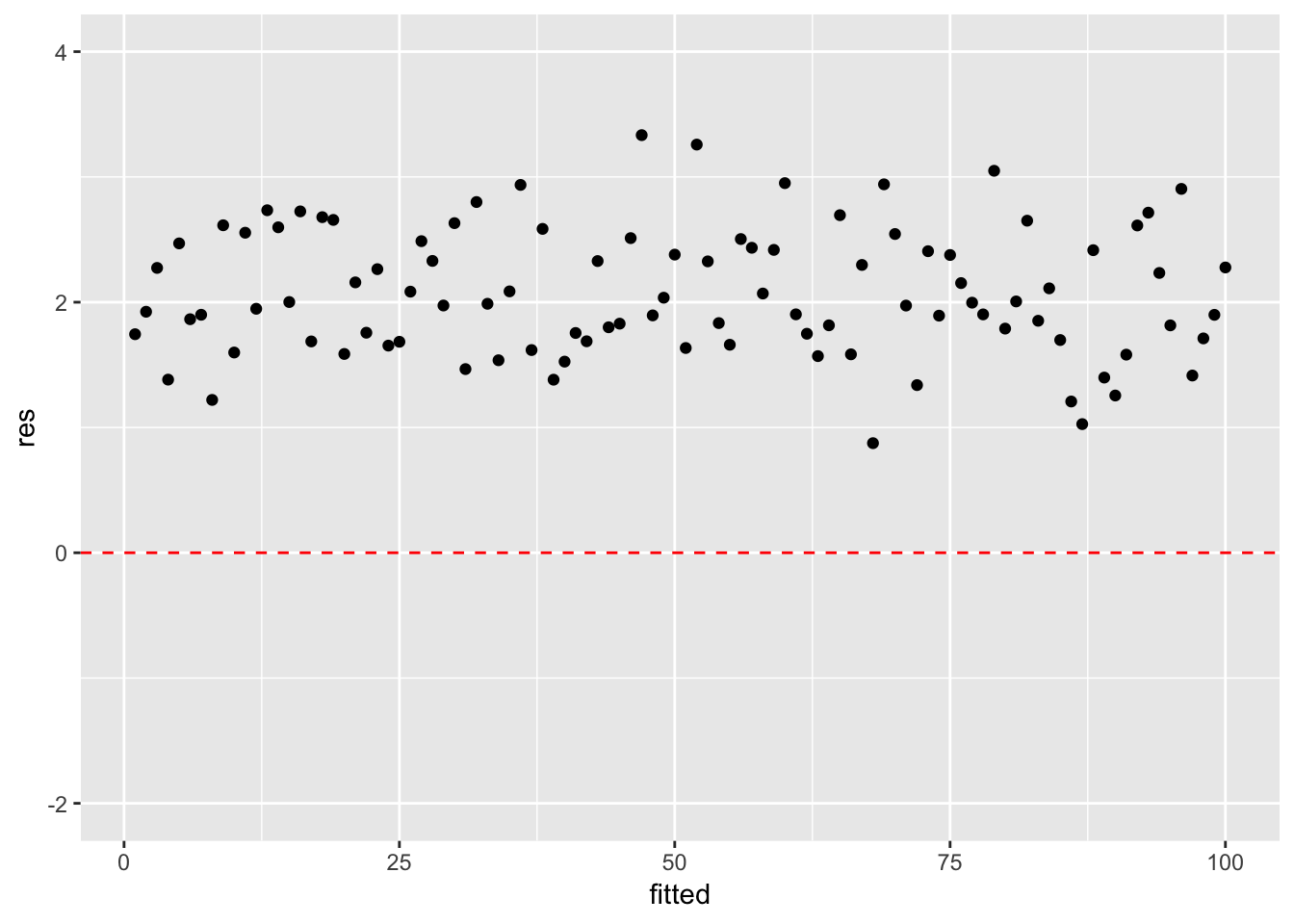
정규성: 잔차의 qqplot을 그려본다, 표준화된 잔차가 0을 중심으로 -3과 3사이에 분포되어있다.
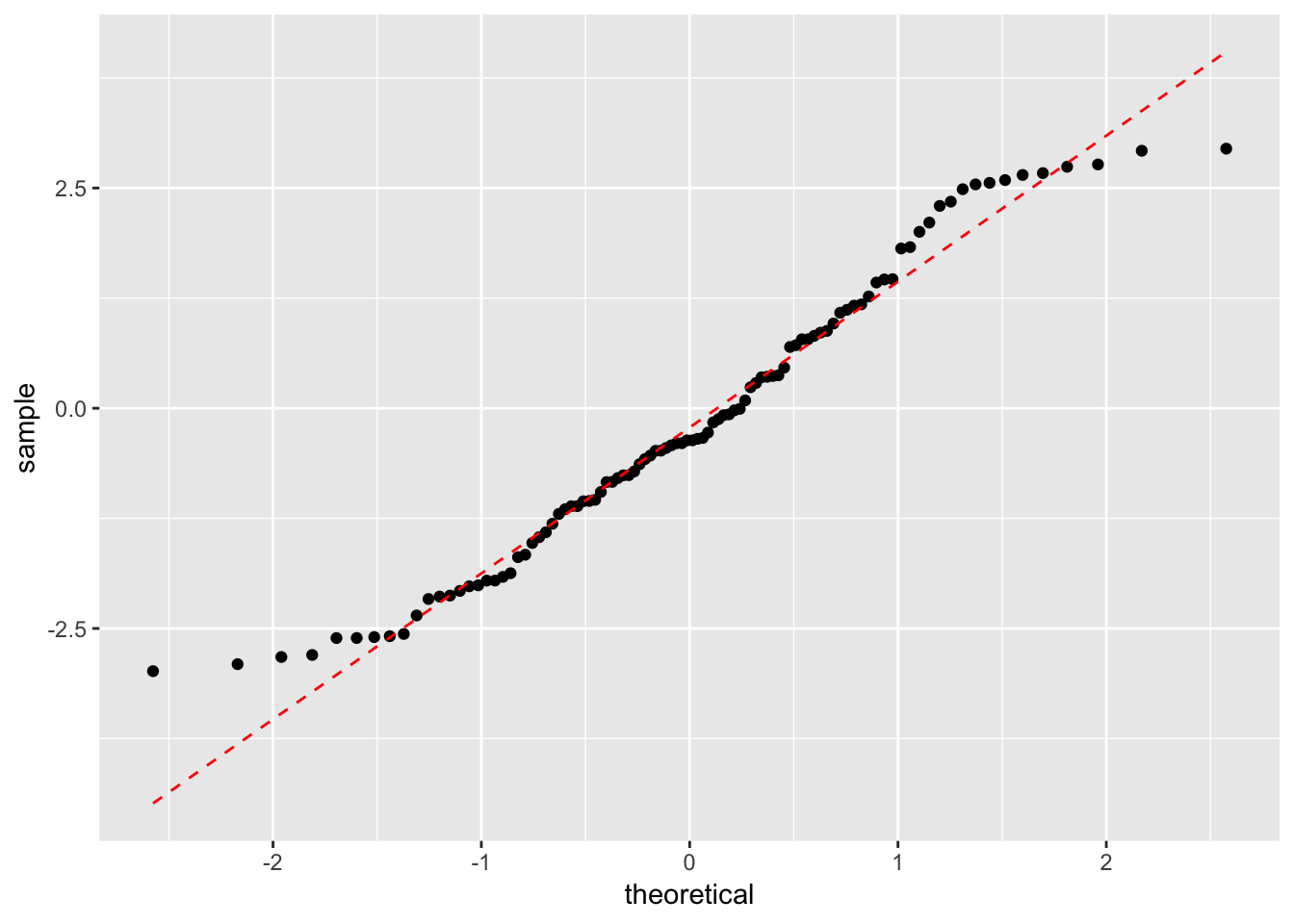
등분산성, 독립성: 잔차의 분포에 특별한 규칙성이 존재하지 않는다.
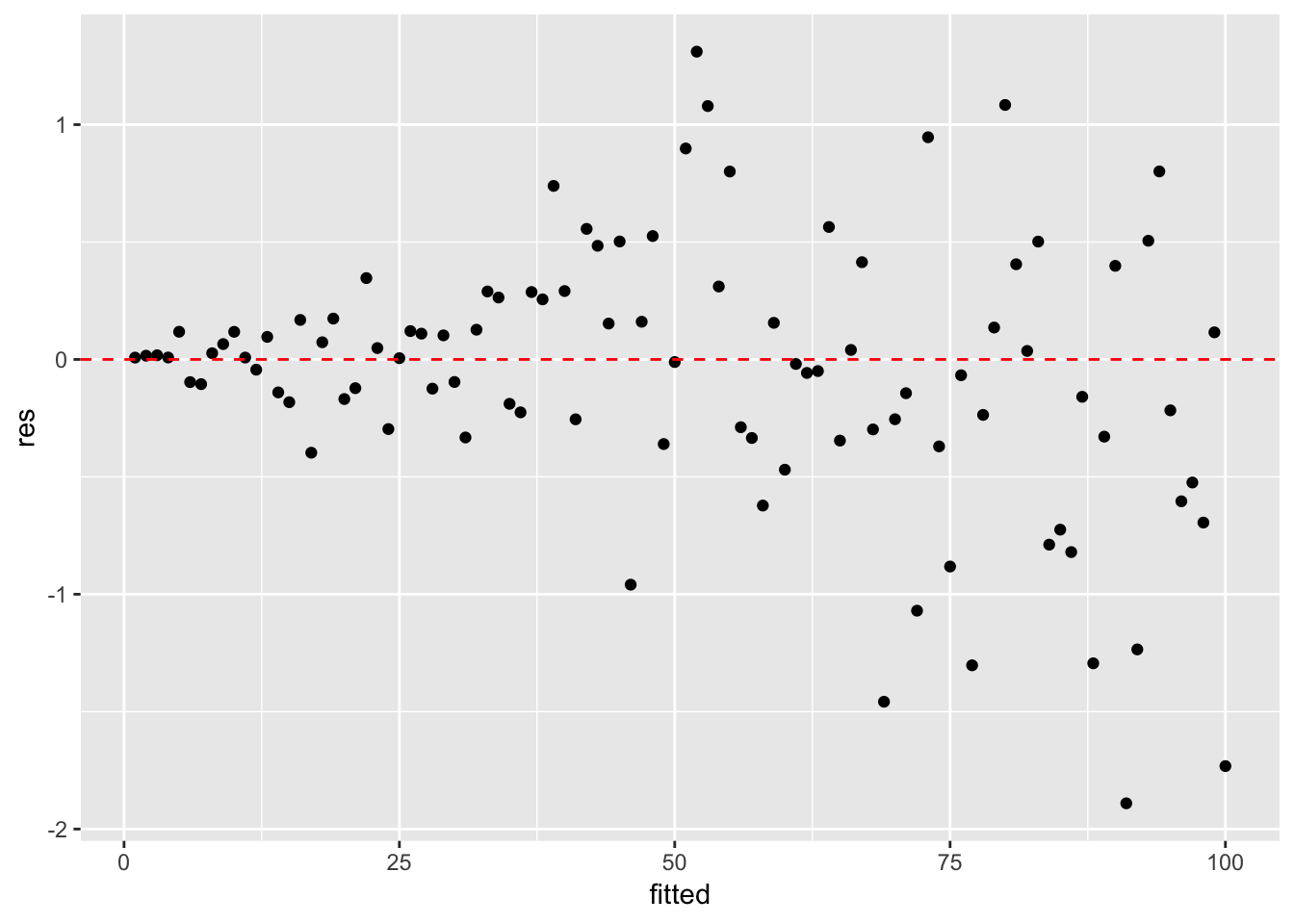
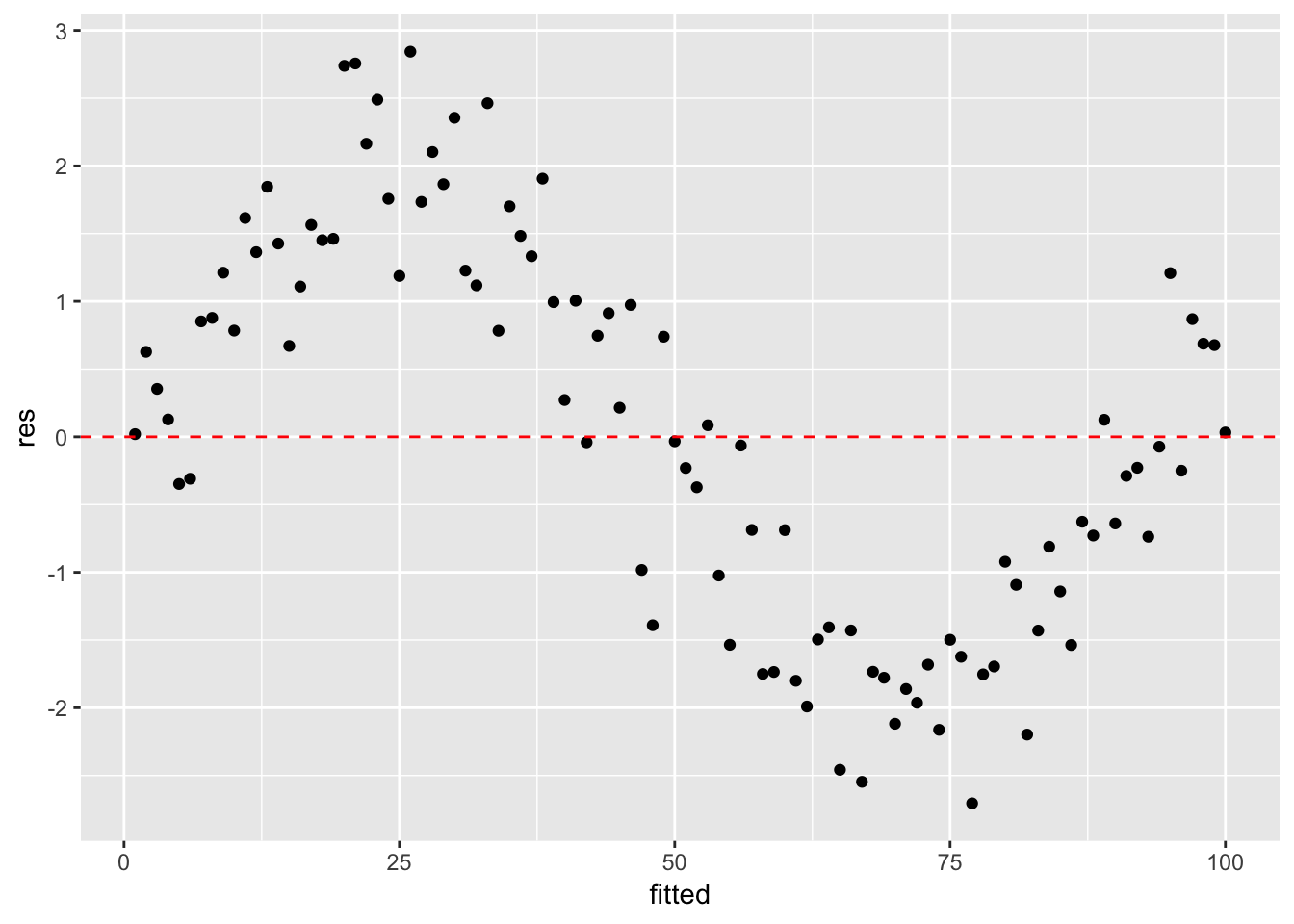
2.2.2 실습
- 적합된 선형회귀모형에 대해
plot()함수를 사용하면 잔차분석을 실시할 수 있다. - 함수의 결과로는 총 네 개의 그래프가 출력이 되는데 그 중 첫 번째 그래프가 잔차도(residual plot), 두 번째 그래프는 잔차의 정규 분위수 그래프(qqplot)이다.
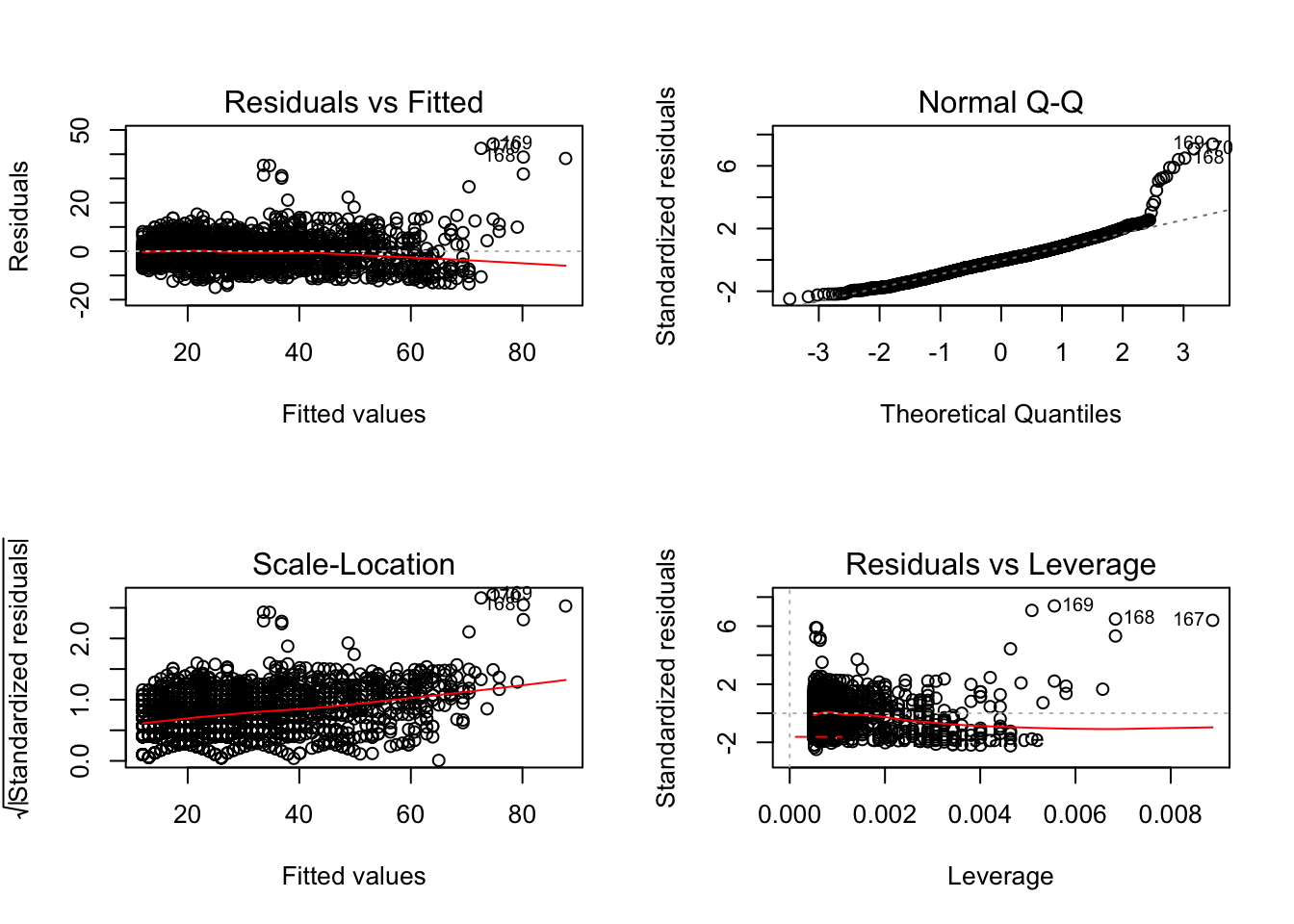
- 잔차도를 확인한 결과, 예측값이 70보다 작거나 같은 값들에서는 회귀모형의 가정에 문제가 없으나, 그 이상의 값들에서는 큰 문제가 있는 것으로 보인다.
- 즉, 단순선형회귀모형의 적용은 타당하지 않음을 뜻한다.
2.3 중회귀분석
2.3.1 중회귀모형
- 중회귀모형이란 설명변수의 개수가 2개 이상인 다음과 같은 모형을 의미한다. \[y = \beta_0 + \beta_1 x_1 + \cdots + \beta_k x_k + \epsilon\]
- 중회귀모형에서도 오차항은 서로 독립이고 평균이 0, 분산이 \(\sigma^2\)으로 동일한 정규분포 \(N(0, \sigma^2)\)을 가정한다.
2.3.2 중회귀모형의 추정(적합)
- 중회귀모형의 회귀계수 또한 단순선형회귀모형과 마찬가지로 최소제곱추정을 이용해 추정한 최소제곱추정량을 사용한다.
- 즉, \(\displaystyle\sum_{i=1}^n (y_i - \beta_0 - \beta_1 x_{1i} - \cdots - \beta_k x_{ki})^2\)을 최소화하는 회귀계수들을 찾는다.
2.3.3 회귀직선의 유의성 검정
- 중회귀모형의 유의성 검정은 다음의 귀무가설에 대한 검정으로 이루어진다. \[H_0: \beta_1 = \cdots = \beta_k = 0, \quad \text{vs} \quad H_1: \text{ not } H_0\]
- 단순선형회귀모형과 마찬가지로, 중회귀모형의 유의성 검정도 ANOVA table 을 이용해 실시한다.
- 중회귀모형에서는 \(SSR\)과 \(SSE\)의 자유도가 \(k\), \(n-k-1\)이다.
2.3.4 결정계수와 수정된 결정계수
- 중회귀모형의 결정계수 \(R^2 = \dfrac{SSR}{SST} = 1 - \dfrac{SSE}{SST}\)는 회귀직선에 포함된 변수가 많을수록 증가한다.
- 그러나 실제로는 쓸모없는 변수가 잔차를 줄이는 작용을 할 수 있기 때문에 너무 많은 수의 변수를 사용하는 것은 좋지 않은 결과를 내기도 한다.
- 이와 같은 문제를 반영하여, 다음의 수정된 결정계수 adjusted \(R^2=1-\dfrac{n-1}{n-k-1} \dfrac{SSE}{SST}\)를 사용하기도 한다.
2.3.5 실습
- 관악구의 미세먼지 자료에는 이산화황
SO2, 일산화탄소CO, 이산화질소NO2변수도 함께 저장되어있다.
## [1] "지역" "측정소코드" "측정소명" "측정일시" "SO2"
## [6] "CO" "O3" "NO2" "PM10" "PM25"
## [11] "주소" "do" "gun"- 이 변수들이 초미세먼지 농도와 어떤 관계가 있는지를 살펴보자.
2.3.5.1 자료 확인
- 먼저, 다음과 같이 자료들을 뽑아 저장하자.
plot()함수에 data frame 을 입력하면 전체 변수에 대한 산점도를 그려준다.
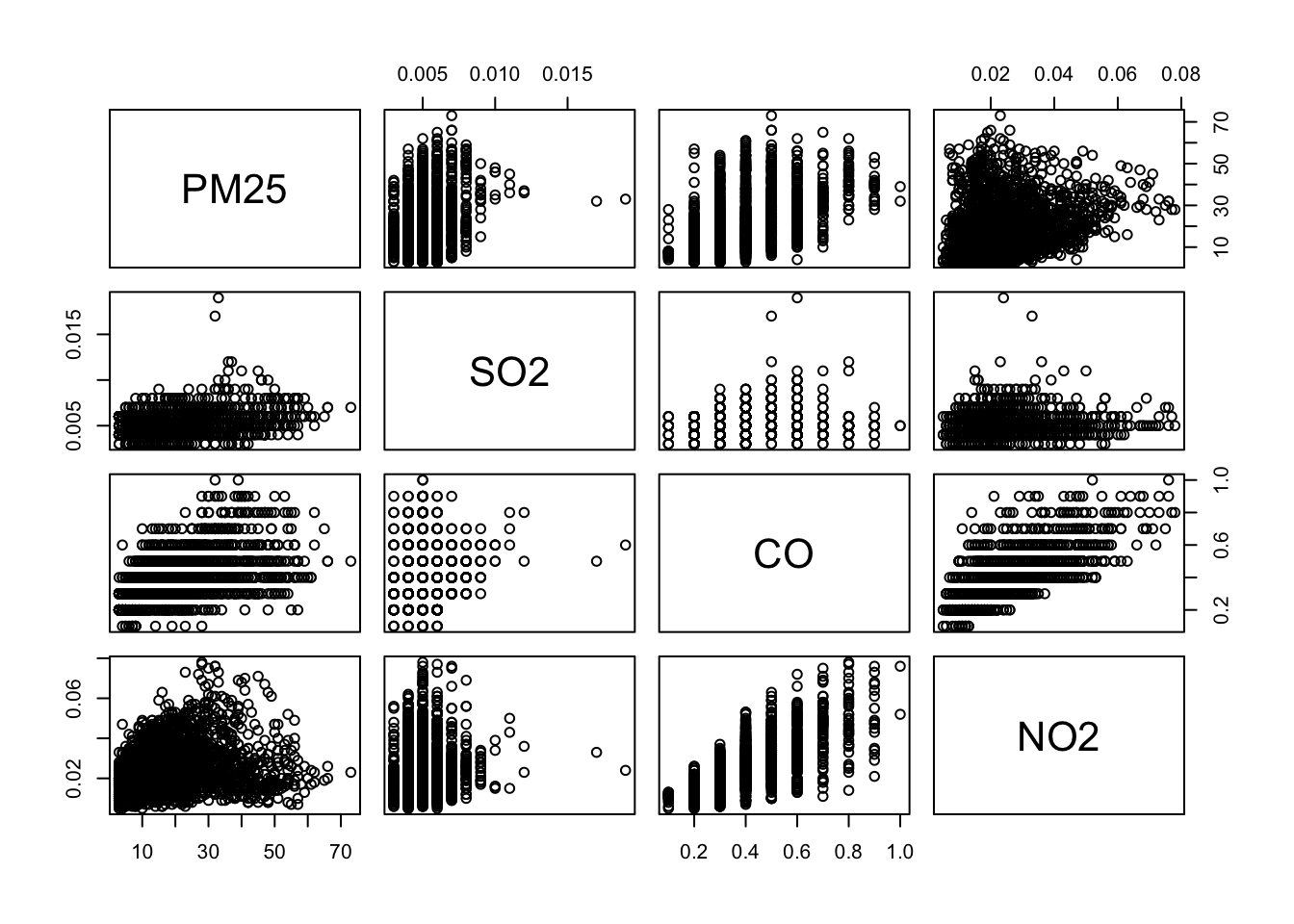
- 다음과 같이 상관계수를 계산할 수도 있다.
## PM25 SO2 CO NO2
## PM25 1.00 0.259 0.55 0.215
## SO2 0.26 1.000 0.13 0.029
## CO 0.55 0.129 1.00 0.712
## NO2 0.21 0.029 0.71 1.000PM25변수와CO변수에는 어느 정도 선형 관계가 존재하는 것처럼 보이지만 나머지는 그렇지 않다.- 상관계수를 확인해보면
PM25와CO변수에는 유의미한 상관관계가 있다고 말할 수 있다.
##
## Pearson's product-moment correlation
##
## data: airdata$PM25 and airdata$CO
## t = 30, df = 2000, p-value <2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.52 0.58
## sample estimates:
## cor
## 0.552.3.5.2 적합
- 중회귀분석을 통해서 반응변수인
PM25가 다른 설명변수들과 어떤 관련성이 있나 살펴보자. - 단순선형회귀분석과 마찬가지로
lm()함수를 사용하고 여러 개의 설명변수를+기호로 연결하여 차례대로 입력할 수 있다.
- 또는 다음과 같이
.을 사용하여 반응변수를 제외한 모든 변수를 설명변수로 사용할 수 있다.
2.3.5.3 결과 확인
summary()를 이용하여 결과를 출력하면 다음과 같다.
##
## Call:
## lm(formula = PM25 ~ ., data = airdata)
##
## Residuals:
## Min 1Q Median 3Q Max
## -25.67 -6.96 -2.15 5.17 43.71
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -6.47 1.07 -6.02 0.0000000021 ***
## SO2 1746.43 182.17 9.59 < 2e-16 ***
## CO 68.25 2.22 30.78 < 2e-16 ***
## NO2 -374.64 27.32 -13.71 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 10 on 1975 degrees of freedom
## Multiple R-squared: 0.399, Adjusted R-squared: 0.398
## F-statistic: 436 on 3 and 1975 DF, p-value: <2e-16- 모형의 유의성 검정에서 검정통계량 \(F = 436.33\)이고 유의확률이 매우 작은 값으로 계산되었다. 따라서, 유의수준 5%에서 모형은 유의하다고 할 수 있다.
- 결정계수 값은 \(R^2 = 0.4\)로 자료의 전체 변동 중 약 40% 정도를 회귀모형이 설명한다고 말할 수 있다.
- 각 계수의 유의성 검정 결과 모든 계수가 유의한 것으로 나타났다.
2.3.5.5 잔차분석
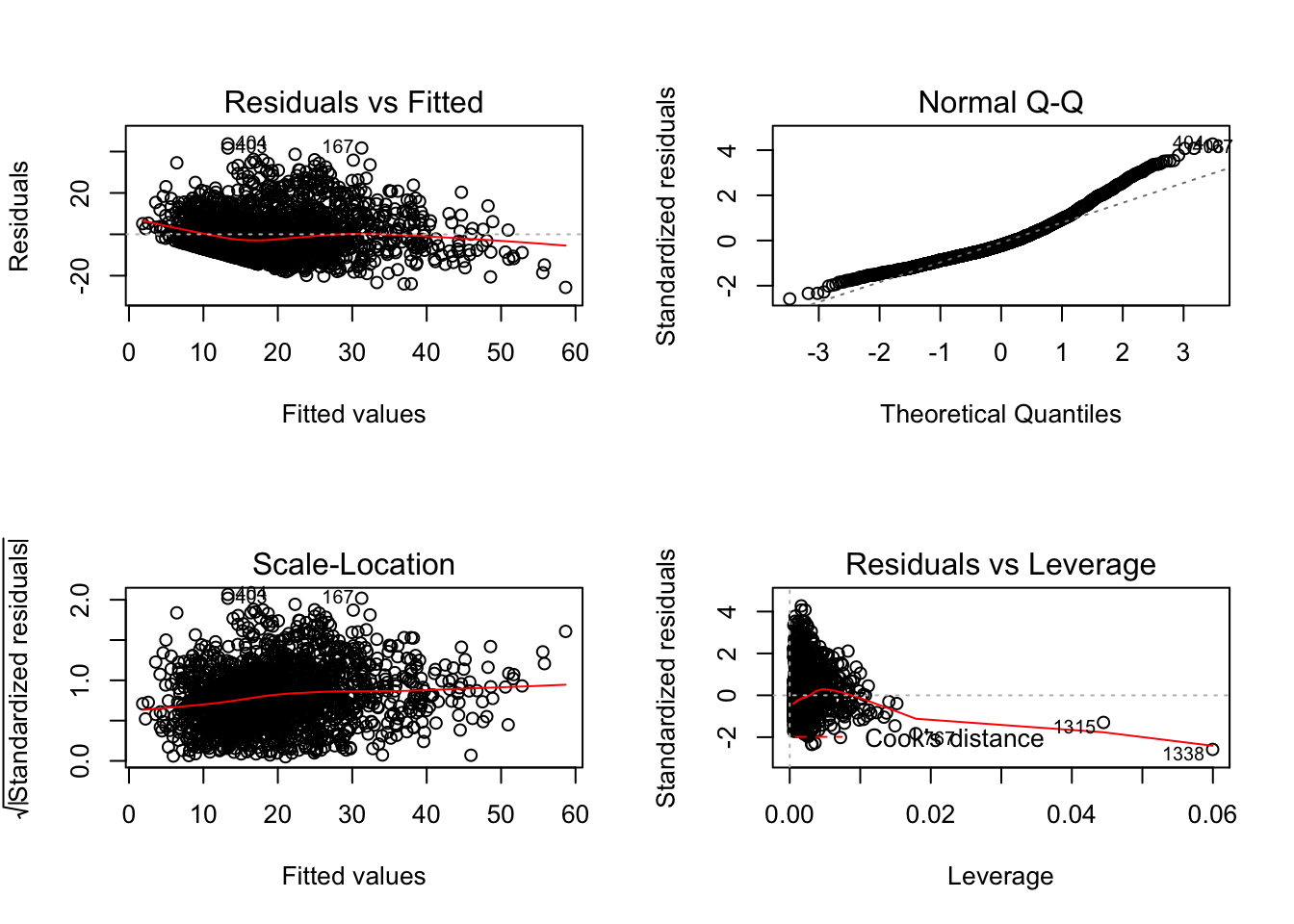
- 적합된 모형의 잔차도를 확인해보면 정규성을 제외한 모형의 가정은 타당하다고 말할 수 있다.
과제
There is no homework!