통계적 추정
2018 가을학기 통계학실험 010 강좌
이경원
October 23, 2018
1 추론 통계학
1.1 추론 통계학
- 추론 통계학은 모집단에 대한 어떤 미지의 양상을 알기 위해 통계학을 이용하여 추측하는 과정을 지칭한다.
- 모집단에 대한 추론을 100% 확신하기 위해서는 모집단 전체를 표본으로 조사해야 한다.
- 그러나 비용 또는 시간 등의 이유로 불가능한 경우가 많기 때문에 표본에서 얻은 정보를 가지고 추론한다.1
 |
|---|
| 추론 통계학, Source: lumenlearning |
1.2 추론 통계학의 종류
추론 통계학은 다시 추정과 검정으로 분류할 수 있다.
- 추정(Estimation)은 표본을 통해 모집단 특성이 어떠한가에 대해 추측하는 과정이다.
- 검정(Testing)은 모집단 실제값이 얼마나 되는가 하는 주장과 관련해서, 표본이 가지고 있는 정보를 이용해 가설이 올바른지 그렇지 않은지 판정하는 과정을 나타낸다.
2 점추정
- 점추정(point estimation)은 하나는 모수를 한 개의 값으로 추정하는 과정을 뜻한다.
- 모수의 추정값을 _추정량_이라 한다.
- 예를 들어, 모집단의 평균을 표본으로부터 계산한 표본평균으로 추정할 수 있다.
- 대표적인 점추정은 다음과 같다.
모수 점추정량 모평균 \(\mu\) 표본평균 \(\bar{X}\) 모비율 \(p\) 표본비율 \(\hat{p} = X/n\) 모분산 \(\sigma^2\) 표본분산 \(S^2\)
2.1 불편추정량
좋은 추정량이란 무엇일까?
- 추정하고자 하는 모수를 \(\theta\), 추정량을 \(\hat{\theta}\)라 하자.
- 추정량의 편향(bias)이란 추정량의 평균값과 모수값의 차이 \(\mathbb{E}[\hat{\theta}] - \theta\)를 뜻한다.
- 추정량의 편향이 0일 때 (즉, 모수의 추정량의 기댓값이 추정하고자 하는 모수가 될 때), 이 추정량을 불편추정량(unbiased estimator)이라 한다.
- 위에서 언급한 점추정량들은 모두 각 모수의 불편추정량이다.
2.2 예제
- 다음은 어떤 반의 학생들의 키를 조사해서 얻은 것이다.
169 166.5 171.6 177.5 169.8 175.4 176 172.1 172.7 173 183.1 180.5 173.6 174.5 174.6 165.8 170 176.4 171.7 174 - 이로부터 학생들의 키의 평균, 분산을 추정한 것은 다음과 같다.
studenth <- c(169, 166.5, 171.6, 177.5, 169.8, 175.4, 176,
172.1, 172.7, 173, 183.1, 180.5, 173.6, 174.5,
174.6, 165.8, 170, 176.4, 171.7, 174)
mean(studenth) ## [1] 173.39## [1] 17.99147sd함수를 통해 모표준편차를 추정해볼 수도 있다.
## [1] 4.241636## [1] 4.241636참고: 표본표준편차 \(S\)는 모표준편차 \(\sigma\)의 불편추정량이 아니다.
- 이때
sd함수는 모표준편차가 아닌 표본표준편차를 계산함에 주의하자.
## [1] 3.02765## [1] 3.02765## [1] 2.8722813 구간추정
- 구간추정(interval estimation)이란 모수가 포함되리라 기대되는 구간으로 모수를 추정하는 방법을 말한다.
- 신뢰구간(confidence interval)은 통계량 \(L\)과 \(U\)에 대하여 \(P(L<\theta<U)=1-\alpha\)을 만족하는, 구간 \((L,U)\) 또는 \((l,u)\)를 뜻한다. 이러한 구간을 \(\theta\)의 신뢰수준 \(100(1-\alpha)\%\)신뢰구간이라 한다
- 위의 정의에서, \(l\)과 \(u\)를 각각 신뢰구간의 하한과 상한, \(1-\alpha\)를 신뢰수준이라 한다.
- 신뢰수준은 100개의 신뢰구간 가운데 약 \(100(1-\alpha)\)개가 모수 \(\theta\)를 포함하리라 기대된다는 의미이다.
참고: 빈도론적 통계학에서 신뢰수준은 “모수가 신뢰구간에 포함될 확률”이 아니다.
3.1 예
- 모분포가 정규분포 \(N(\mu,\sigma^2)\)일 때 모평균 \(\mu\)의 \(100(1-\alpha)\%\)신뢰구간은 다음과 같이 주어진다. \[\left(\bar{x}-z_{\alpha/2}\frac{\sigma}{\sqrt{n}},\bar{x}+z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \right)\]
- 여기서 \(z_{\alpha}\)는 표준정규분포의 \(\alpha\) 상방분위수를 뜻한다.
- 가령, \(\alpha = 0.05\)일 때 \(z_{alpha/2}\)는 1.959964이다.
3.2 신뢰수준의 의미
표준정규분포에서 50개의 난수를 발생시켜 95% 신뢰구간을 구하는 과정을 1000번 반복 하자. 1000개의 신뢰구간 중에서 실제로 모수를 포함하는 신뢰구간의 비율을 구하여라.
## parameters
alpha <- 0.05
n <- 50
mu <- 0
sigma <- 1
count <- 0
set.seed(100)
for (i in 1:1000) {
x <- rnorm(n, mu, sigma) # sampling
upper <- mean(x)-qnorm(alpha/2)*(sigma/sqrt(n)) # ci
lower <- mean(x)+qnorm(alpha/2)*(sigma/sqrt(n)) # ci
if ( (lower< mu) & (mu< upper) ) {
count = count + 1 # whether ci contains mu
}
}
count/1000## [1] 0.9444 가설검정
먼저 가설검정의 기본 용어는 다음과 같다.
- 귀무가설(\(H_0\)): 기존의 가설, 대립가설에 대한 확실한 근거가 없다면 채택되는 가설
- 대립가설(\(H_1\)): 표본으로부터 입증하고자 하는 가설
- 검정: 모집단 실제값이 얼마나 되는가 하는 주장과 관련해서, 표본이 가지고 있는 정보를 이용해 귀무가설이 올바른지 그렇지 않은지 판정하는 과정
- 검정통계량 : 검정에 사용하는 통계량
- 유의수준 : 귀무가설이 참일 때 대립가설을 채택하는 오류를 범할 확률
- 기각역 : 귀무가설을 기각시키는 검정통계량의 관측값의 영역
4.1 검정의 오류와 검정력
- 가설검정에서 발생하는 오류의 종류는 다음과 같다.
- 제1종 오류 (type 1 error): 실제론 귀무가설이 참인데도 검정 결과 대립가설을 채택하는 오류
- 제2종 오류 (type 2 error): 실제론 대립가설이 참인데도 검정 결과 귀무가설을 채택하는 오류
- 이를 표로 정리하면 다음과 같다.
\(H_0\) 참 \(H_1\) 참 검정 결과 \(H_0\) 채택 옳은 결정 제2종 오류 \(H_1\) 채택 제1종 오류 옳은 결정
유의수준, 유의확률, 검정력은 다음과 같이 정의된다.
- 유의수준 (\(\alpha\)): 귀무가설 \(H_0\)가 참일 때 대립가설 \(H_1\)을 채택하는 오류를 범할 최대 허용 확률 (= 제 1종의 오류를 범할 확률)
- 유의확률 (p-value): 귀무가설이 맞다고 가정할 때 얻은 결과보다 (대립가설의 방향으로) 극단적인 결과가 실제로 관측될 확률이다. 유의확률이 작을수록 대립가설 \(H_1\)이 참이라는 증거가 강함을 뜻한다.
- 검정력 : 대립가설 특정 값에서 귀무가설 \(H_0\)를 기각시킬 확률. 검정력이 높을 수록 좋은 검정이라 할 수 있다.
유의확률은 대립가설이 참일 확률이 아니다.
4.2 예
모표준편차 \(\sigma\)가 알려져 있을 때, 귀무가설 \(H_0:~\mu = \mu_0\)에 대한 표본평균을 이용한 모평균의 검정은 다음의 Z-검정을 사용한다.
- 검정통계량 : \(Z=\dfrac{\bar{X}-\mu_0}{\sigma/\sqrt{n}}\)
- 대립가설에 따른 기각역과 검정통계량 \(z_0\)에 대한 유의확률 계산 :
| 가설 | 기각역 | 유의확률 |
|---|---|---|
| \(H_1\): \(\mu\) > \(\mu_0\) | \(Z \geq z_{\alpha}\) | \(\mathbb{P}(Z \geq z_0)\) |
| \(H_1\): \(\mu\) < \(\mu_0\) | \(Z \leq z_{\alpha}\) | \(\mathbb{P}(Z \leq z_0)\) |
| \(H_1\): \(\mu \neq \mu_0\) | \(|Z| \geq z_{\alpha/2}\) | \(\mathbb{P}(|Z| \geq |z_0|)=2 \mathbb{P}(Z \geq |z_0|)\) |
4.3 예제
어느 전구의 평균수명이 정규분포 \(N(1500,100^2)\)을 따른다고 하자. 이 때, 새 공법에 의하면 전구의 평균수명이 증가한다고 할 때, \(n=25\)개의 전구를 시험 생산한 결과 \(\bar{X}= 1550\) (시간)으로 나타났다. 이 결과를 통해 새 공법에 의해 전구의 평균수명이 증가했다고 확신할 수 있는가? 유의수준 5%에서 이를 확인하시오.
주어진 문제에서 다음과 같이 가설을 설정하자. \[H_0 : \mu=1500 \quad \text{vs} \quad H_1: \mu>1500\] 모표준편차가 알려져 있으므로, 검정통계량은 \[Z=\frac{\bar{X}-1500}{100/\sqrt{n}} = \frac{1550-1500}{20}=2.5\] 로 계산되고 유의수준 5%에서 기각역은 \(Z>1.645\), 검정통계량이 기각역에 속하므로 귀무가설을 기각할 수 있다. 즉, 유의수준 5%에서 새 공법에 의해 전구의 평균수명이 증가했다고 확신할 수 있다. R을 이용해서는 다음과 같이 유의확률을 계산할 수 있다.
## [1] 2.5## [1] 0.006209665## [1] 0.006209665과제
- 주어진 자료는 Iowa의 도시 Ames의 2006년부터 2010년 사이의 부동산 거래내역 자료이다.
- 5년 동안 이 지역에서 발생한 총 2930건의 부동산 거래내역이 모두 기록되어 있다.
- 자료에 대한 설명은 다음과 같다. (http://www.openintro.org/stat/data/?data=ames)
All residential home sales in Ames, Iowa between 2006 and 2010. The data set contains many explanatory variables on the quality and quantity of physical attributes of residential homes in Iowa sold between 2006 and 2010. Most of the variables describe information a typical home buyer would like to know about a property (square footage, number of bedrooms and bathrooms, size of lot, etc.). A detailed discussion of variables can be found in the original paper referenced below.
- 다음 링크에서 csv 파일을 다운로드 받은 뒤, 다음과 같이 자료를 불러오자.
- 본 과제에서는 집의 크기를 나타내는 변수인
Gr.Liv.Area를 모집단으로 사용하기로 하자. - 먼저 다음과 같이
Gr.Lib.Area변수를GLA에 저장하자.
1번
(a)
- 주어진 자료를 통해 전체 부동산의 집의 크기의 모평균값을
muGLA, 모분산 \(\sigma^2\)값을varGLA변수에 저장하여라.
(b)
- 모집단에서 크기가 60인 랜덤 표본을 선택하고(복원추출), 모평균값의 점추정량을
meanGLA변수에 저장하여라.
Solution
- 모평균값의 점추정량으로는 표본평균을 사용할 수 있다.
- 크기가 60인 표본을 추출하고 표본평균을 계산하는 코드는 다음과 같다.
(c)
- 앞에서 선택한 표본을 이용하여 모평균에 대한 95% 신뢰구간을 구하고, 이 구간의 하한과 상한을
ciGLA변수에 저장하여라. (모분산은 a에서 구한 값을 이용한다.) - 가령, 신뢰구간이 \((10,15)\)로 계산되었다면 다음과 같이 저장하면 된다.
Solution
- 다음과 같이 신뢰구간을 계산할 수 있다.
z_alpha <- qnorm(0.025,0,1,lower.tail = F)
sampsize <- length(sampGLA)
ciGLA <- c(
meanGLA - z_alpha * sqrt(varGLA) / sqrt(sampsize),
meanGLA + z_alpha * sqrt(varGLA) / sqrt(sampsize)
)
ciGLA## [1] 1328.529 1584.304(d)
- c번과 동일한 과정을 50번 반복하여 서로 다른 신뢰구간 50개를 구해보자. 이 때, 각 신뢰구간의 하한값을
lower벡터에 각각 저장하고 각 신뢰구간의 상한값은upper벡터에 각각 저장하도록 한다.
Solution
set.seed(100)
n <- 60
N <- 50
lower <- numeric(N)
upper <- numeric(N)
z_alpha <- qnorm(0.025,0,1,lower.tail = F)
sdGLA <- sqrt(varGLA)
for(i in 1:N) {
samp <- sample(GLA, n, replace=T)
sampmean <- mean(samp)
lower[i] <- sampmean - z_alpha * sdGLA / sqrt(n)
upper[i] <- sampmean + z_alpha * sdGLA / sqrt(n)
}(e)
제출하지 않아도 됩니다. (채점되지 않는 문항입니다.)
- 아래의 코드를 실행해보자.
## draw base plot
k <- length(lower)
max_ci_length <- max(upper - lower)
xrange <- muGLA + max_ci_length * c(-1, 1)
yrange <- c(0, k+1)
plot(xrange, yrange, type = 'n', xlab = '', ylab = '', axes = F)
abline(v = muGLA, lty = 2, col = 'red')
axis(1, at = muGLA, paste0("mu = ", round(muGLA, 4)), tick = F)
# draw cis
for (i in 1:k) {
ci <- c(lower[i], upper[i])
ci_mean <- mean(ci)
col <- 1 + (ci[1] > muGLA | ci[2] < muGLA)
lines(ci, rep(i, 2), col = col)
points(ci_mean, i, col = col, pch = 16)
}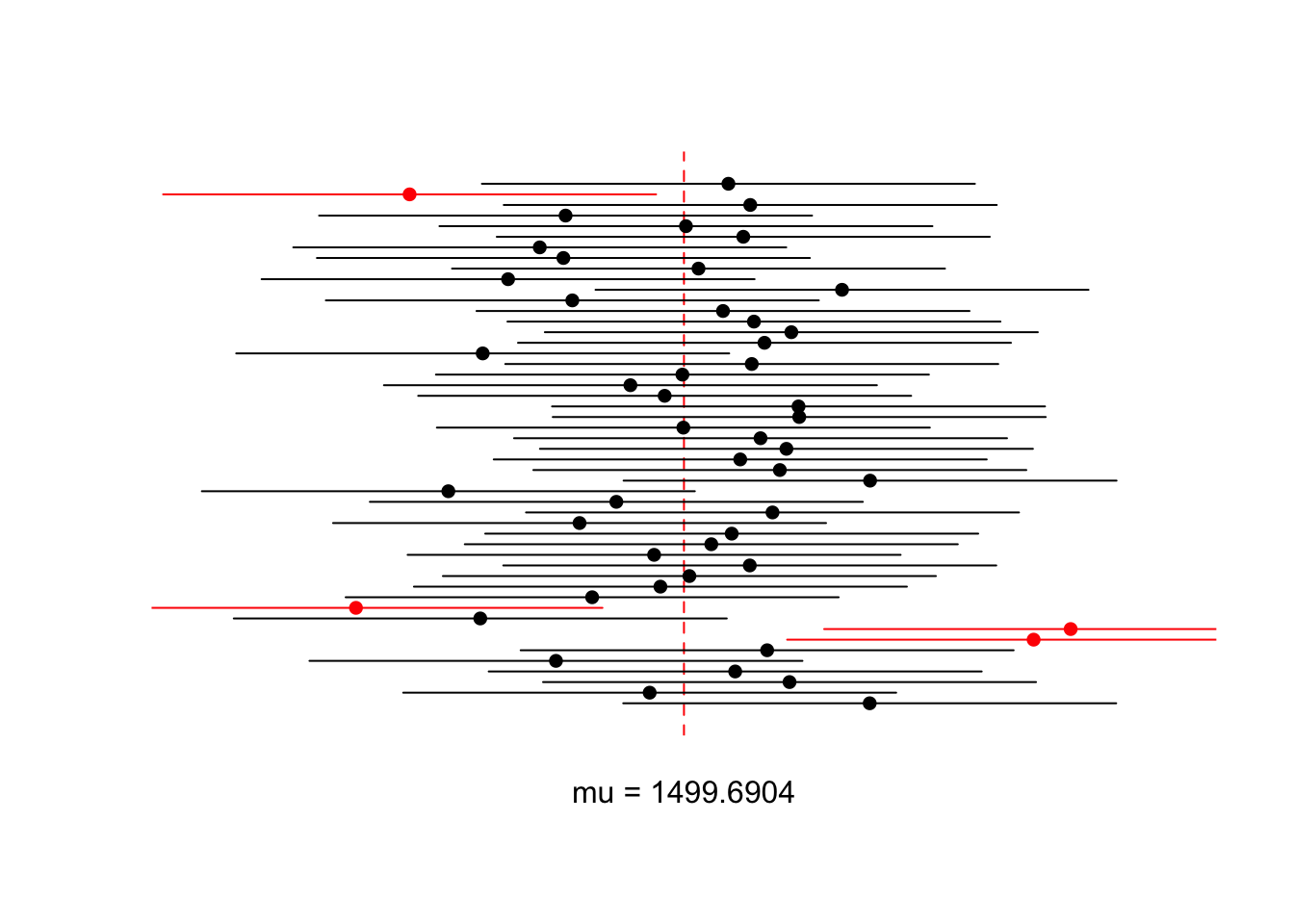
- 위의 문제들을 제대로 풀었다면 위와 비슷한 그래프가 얻어질 것이다.
참고 (20181026 추가)
- 위의 추론과정의 정당화를 위해서는
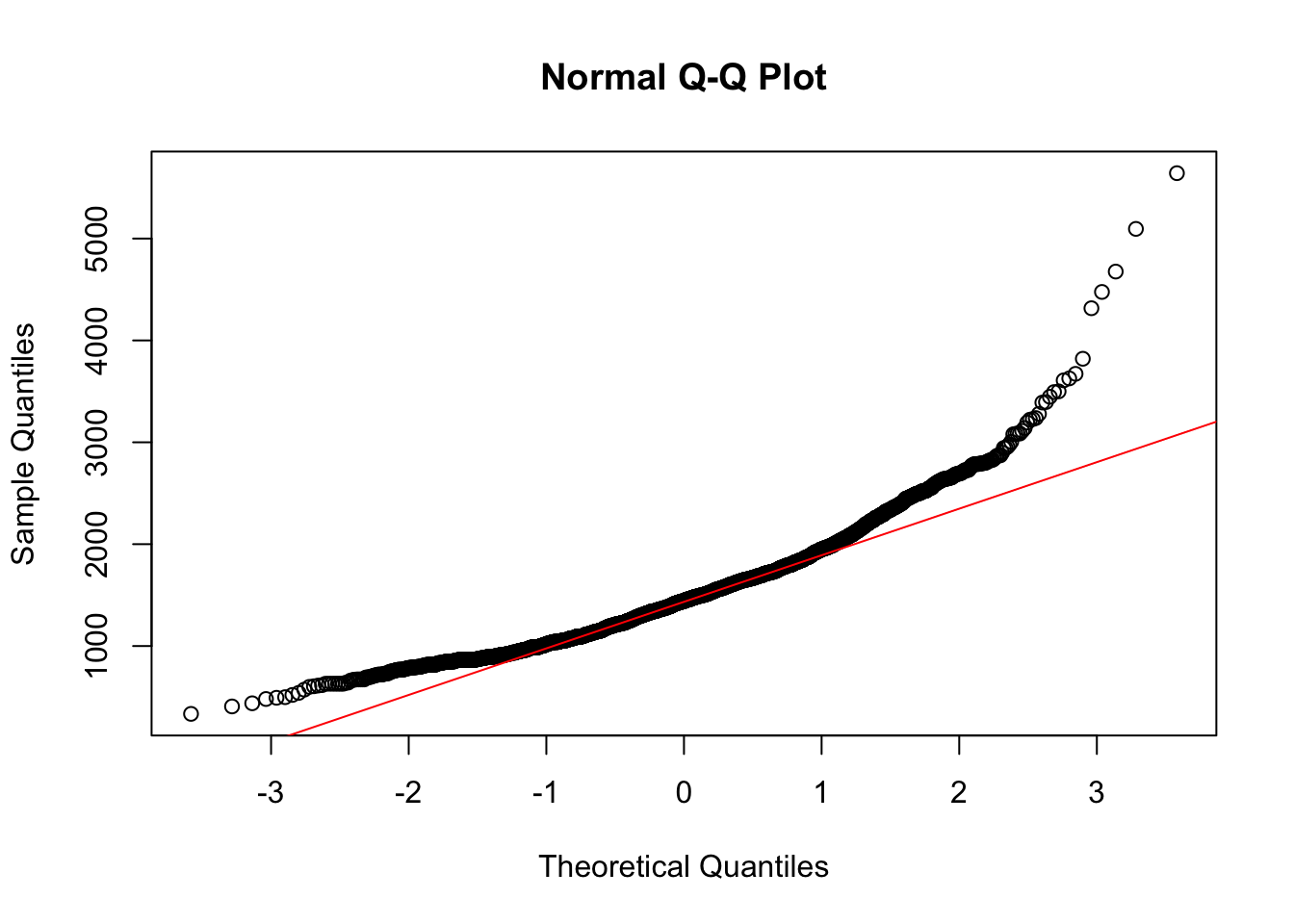
GLA변수가 정규분포를 따른다는 가정이 필요하다. - 그러나, qqplot을 그려보면
GLA변수는 정규모집단이 아니라는 것을 확인할 수 있다. - 이번 문제에서는
GLA가 정규모집단이라는 가정 하에 풀이를 작성하면 된다.