1 기술 통계학

기술 통계학(descriptive statistics)는 측정이나 실험에서 수집한 자료의 정리, 표현, 요약, 해석 등을 통해 자료의 특성을 규명하는 통계적 방법이다.¹


잘못된 기술통계학

2 일변량 자료의 요약

자료의 특성이 한 가지 뿐인 자료를 일변량 자료라 한다.
자료의 특성을 요약하는 방법으로는 히스토램, 도수분포다각형과 같은 그래프를 이용한 요약과 평균, 중앙값 등 수치를 이용한 요약이 있다.
앞 장에서 다루었던 10명의 학생들에 대한 수학, 영어 시험 성적 자료를 생각하자.

나이	성별	수학	영어
19	M	56	76
25	M	74	63
19	F	79	93
24	F	69	99
26	M	68	98
20	F	88	65
24	F	94	74
25	M	54	71
19	F	53	82
25	M	66	75

다음과 같이 자료를 입력하자.

gender <- c("M",'M','F','F','M','F','F','M','F','M')
math <- c(56, 74, 79, 69, 68, 88, 94, 54, 53, 66)

이때 성별 gender 벡터는 범주형 자료이기 때문에, factor() 함수를 사용하여 범주형 요인 변수로 변형하여 사용하자.

gender <- factor(gender)

성별을 입력한 gender 벡터에 factor()함수를 사용하게 되면 gender 벡터는 M, F 의 두 가지 값을 갖는 범주형 자료가 된다.

2.1 그래프를 이용한 요약

그래프를 이용하면 주어진 자료를 시각적으로 요약할 수 있다.

2.1.1 히스토그램

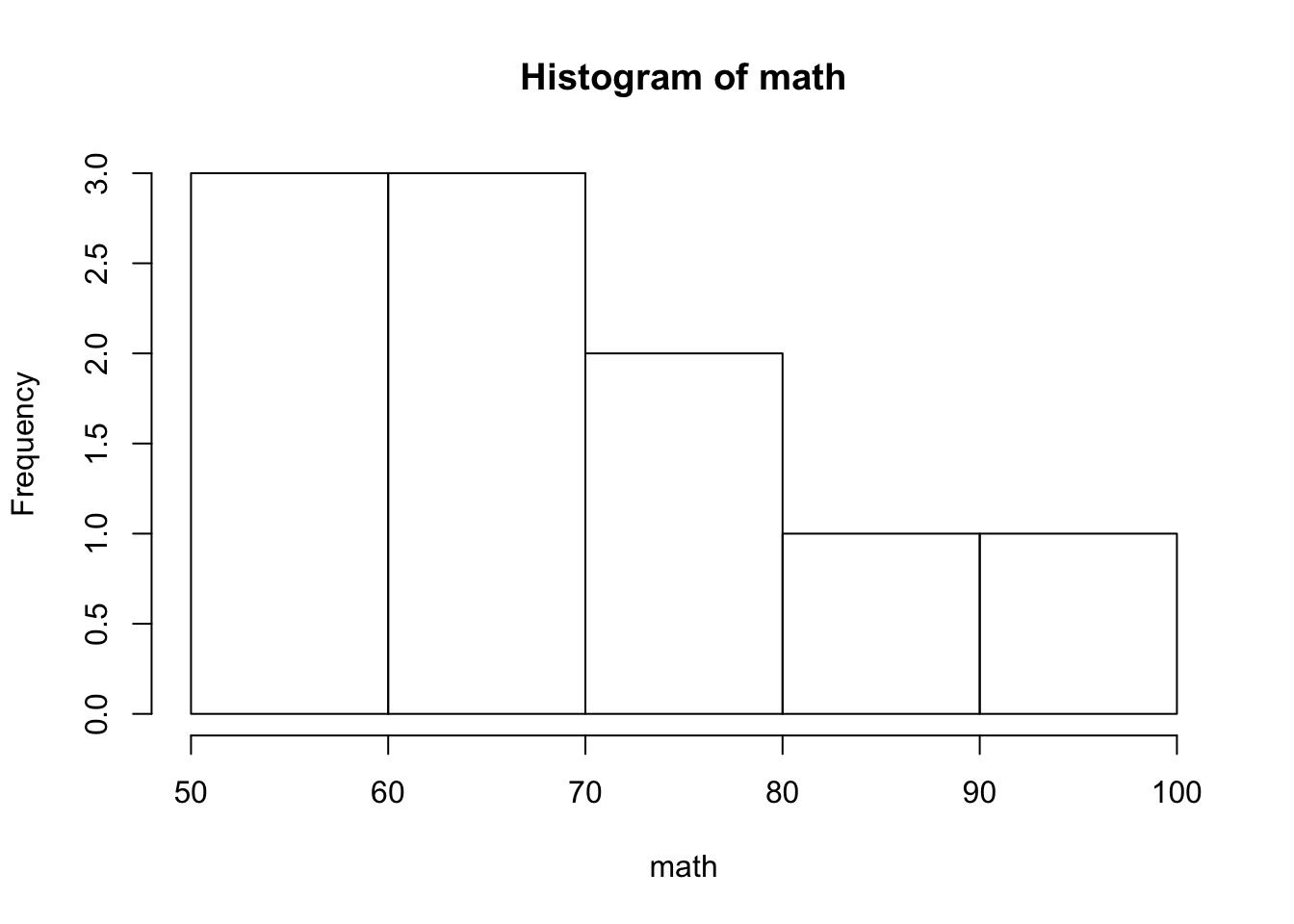
히스토그램(Histogram)은 일변량 자료의 분포를 알아보는데 유용하다.
R에서 히스토그램은 hist() 함수를 이용해 그릴 수 있다.
math 변수의 히스토그램은 다음과 같이 그릴 수 있다.

hist(math)

R의 많은 함수들은 다양한 매개변수(parameter)들을 입력으로 함께 받아 적절한 결과를 출력한다.
별도의 매개변수를 지정하지 않는 경우, 함수의 기본 입력값으로 실행된 결과가 출력된다.
가령, 히스토그램의 모양을 결정짓는 요소로는 막대의 의미 (빈도 혹은 밀도)이 있고, 히스토그램의 제목을 바꿀 수도 있을 것이다.
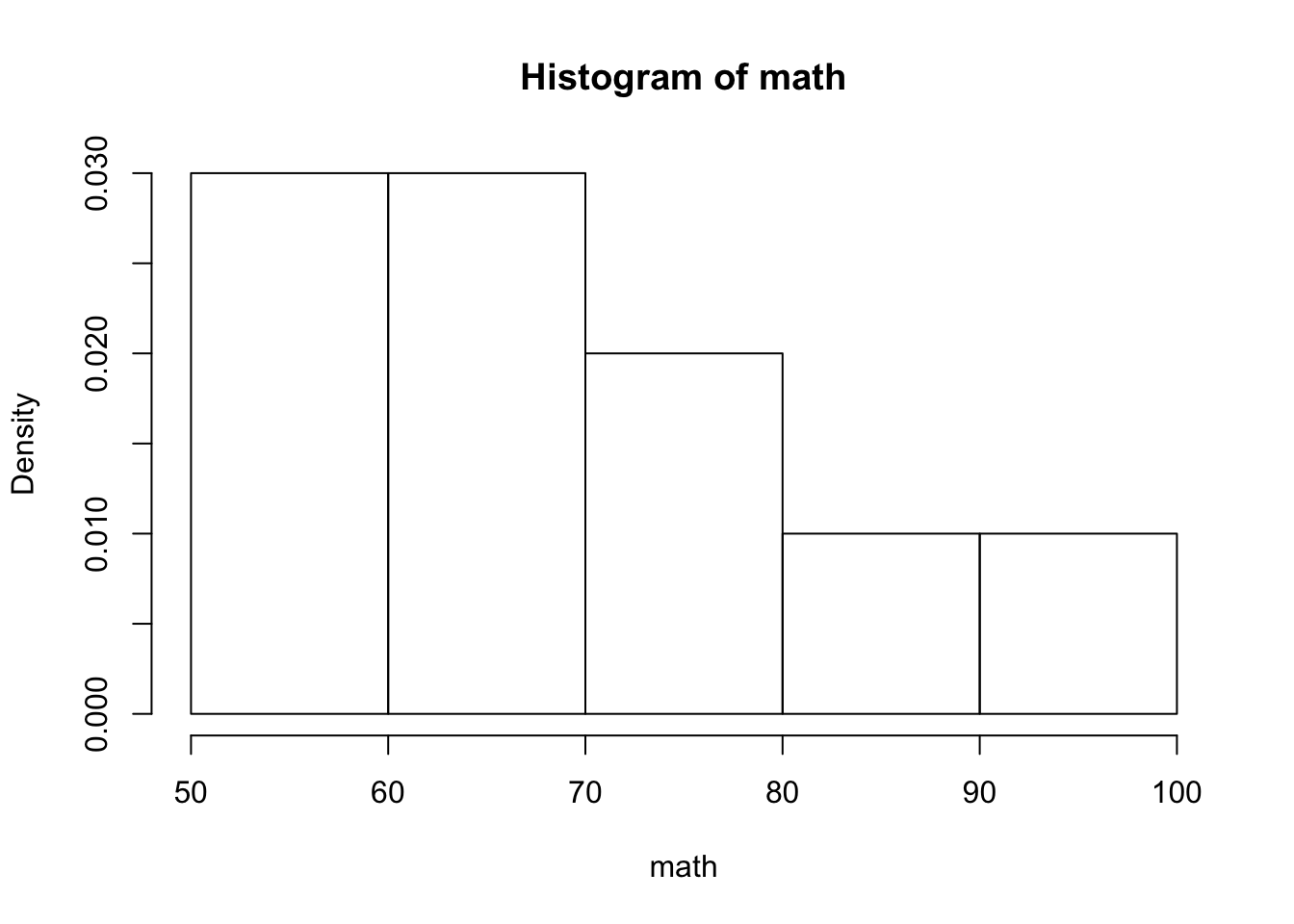
이들은 hist() 함수에서 freq, main 매개변수를 통해 조정할 수 있다.
다음은 math 변수의 밀도를 y축으로 하는 히스토그램을 그리는 코드이다.

hist(math, freq=F)

다음은 제목이 ’Histogram of mathematics’인 히스토그램을 그리는 코드이다.

hist(math,main='Histogram of mathematics')

함수와 매개변수에 대한 설명은 도움말을 이용해 확인할 수 있다.
R에서 함수에 대한 도움말을 보려면 help(함수명) 또는 ?함수명을 입력하면 된다.

2.1.2 줄기-잎 그림

줄기-잎 그림(Stem-and-leaf plot)은 자료를 표 형태와 그래프 형태의 혼합된 형태로 나타내는 대표적인 방법이다.
줄기는 자료들의 공통되는 부분을, 잎은 줄기 부분의 나머지 부분을 의미한다.
R에서 줄기-잎 그림은 stem() 함수로 그릴 수 있다.
math 변수의 줄기-잎 그림은 다음과 같이 그릴 수 있다.

stem(math)

## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##   5 | 346
##   6 | 689
##   7 | 49
##   8 | 8
##   9 | 4

2.1.3 상자그림

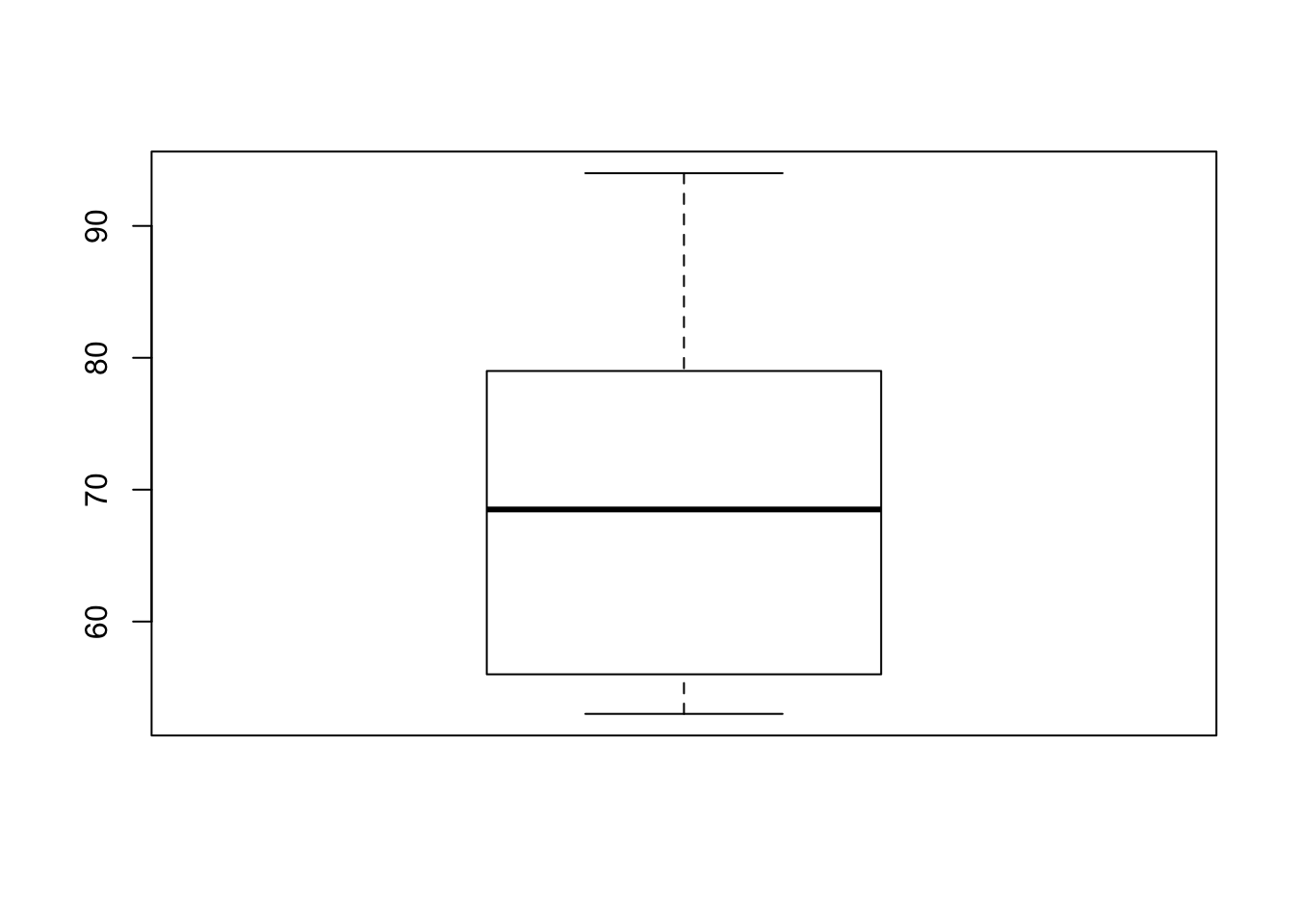
상자그림(Box plot)은 데이터의 분포를 보여주는 그래프로, 가운데 상자는 제1 사분위수($Q_1$), 중앙값($Q_2$; Median), 제3 사분위수($Q_3$) 값을 의미한다.
상자그림은 다음과 같이 그릴 수 있다. ²
1. 주어진 데이터에서 각 사분위수를 계산한다.
2. 그래프에서 $Q_1$, $Q_3$를 밑변으로 하는 직사각형을 그리고, 중앙값에 해당하는 위치에 선분을 긋는다.
3. 사분위수 범위(IQR, Interquartile range, $Q_3−Q_1$)을 계산한다.
4. $Q_3$과 차이가 1.5IQR 이내인 값 중에서 최댓값을 $Q_3$과 직선으로 연결하고, 마찬가지로 $Q_1$과 차이가 1.5IQR 이내인 값 중에서 최솟값을 $Q_1$과 연결한다.
5. $Q_3$보다 1.5IQR 이상 초과하는 값과 $Q_1$보다 1.5IQR 이상 미달하는 값은 점이나, 원, 별표등으로 따로 표시한다(이상치 점).
R에서 상자그림은 boxplot() 함수로 그릴 수 있다.
math 변수의 상자그림은 다음과 같이 그릴 수 있다.

boxplot(math)

2.2 수치를 이용한 요약

통계량이란 표본으로부터 계산되는 표본의 특성값을 뜻한다.
통계량을 이용하면 주어진 자료를 수치적으로 요약할 수 있다.
대표적으료 사용되는 통계량은 다음과 같다.
- 자료의 중심에 대한 측도 : 평균, 중앙값
- 자료의 분포에 대한 측도 : 분산, 표준편차, 사분위수범위

2.2.1 범주형 자료의 요약

범주형 자료를 요약하는데 주로 사용되는 통계량으로는 도수가 있다.
도수란, 범주형 자료가 반복된 횟수를 의미하고 이들을 정리한 표를 분할표라 한다.
R에서는 table()함수를 통해 범주형 자료의 분할표를 그릴 수 있다.
gender 변수의 분할표는 다음과 같이 그릴 수 있다.

table(gender)

## gender
## F M 
## 5 5

2.2.2 숫자형 자료의 요약

숫자형 자료를 요약하는데 주로 사용되는 통계량으로는 평균, 중앙값 등이 있다.
R에서는 평균과 중앙값을 각각 mean(), median()함수를 이용해 계산할 수 있다.
math 변수의 평균과 중앙값은 다음과 같이 계산할 수 있다.

mean(math)

## [1] 70.1

median(math)

## [1] 68.5

이 외에도, 주로 쓰이는 함수들은 다음과 같다.

함수	기능
mean	평균
sd	(표본) 표준편차
var	(표본) 분산
median	중앙값
quantile	분위수
sum	합
min	최솟값
max	최댓값

mean(math)

## [1] 70.1

sd(math)

## [1] 13.97975

median(math)

## [1] 68.5

sum(math)

## [1] 701

max(math)

## [1] 94

5가지 요약 수치 (Five-number summary)는 기술통계학에서 자료의 정보를 알려주는 아래의 다섯 가지 수치를 의미한다³
1. 최솟값
2. 제1 사분위수
3. 제2 사분위수 (중앙값)
4. 제3 사분위수
5. 최댓값
5가지 요약 수치는 fivenum()를 이용할 수 있고 summary()는 5가지 요약 수치와 평균을 함께 계산해준다.

fivenum(math)

## [1] 53.0 56.0 68.5 79.0 94.0

summary(math)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   53.00   58.50   68.50   70.10   77.75   94.00

다음과 같이 5가지 요약 수치를 다른 벡터에 저장할 수도 있다.

five_math <- fivenum(math)
five_math

## [1] 53.0 56.0 68.5 79.0 94.0

3 이변량 자료의 요약

자료의 특성이 두 가지인 자료를 이변량 자료, 두 가지 이상인 자료를 다변량 자료라 한다.
여기서는 이변량 자료를 요약하는 방법에 대해서 알아보기로 한다.
다음과 같이 나이와 영어 성적을 각각 age, eng에 저장하자.

age = c(19, 25, 19, 24, 26, 20, 24, 25, 19, 25)
eng = c(76, 63, 93, 99, 98, 65, 74, 71, 82, 75)

3.1 그래프를 이용한 요약

3.1.1 산점도

그래프를 이용한 이변량 자료의 요약은 산점도(scatter plot)를 이용할 수 있다.
R에서는 plot() 함수를 이용하면 산점도를 그릴 수 있다.

plot(age, eng)

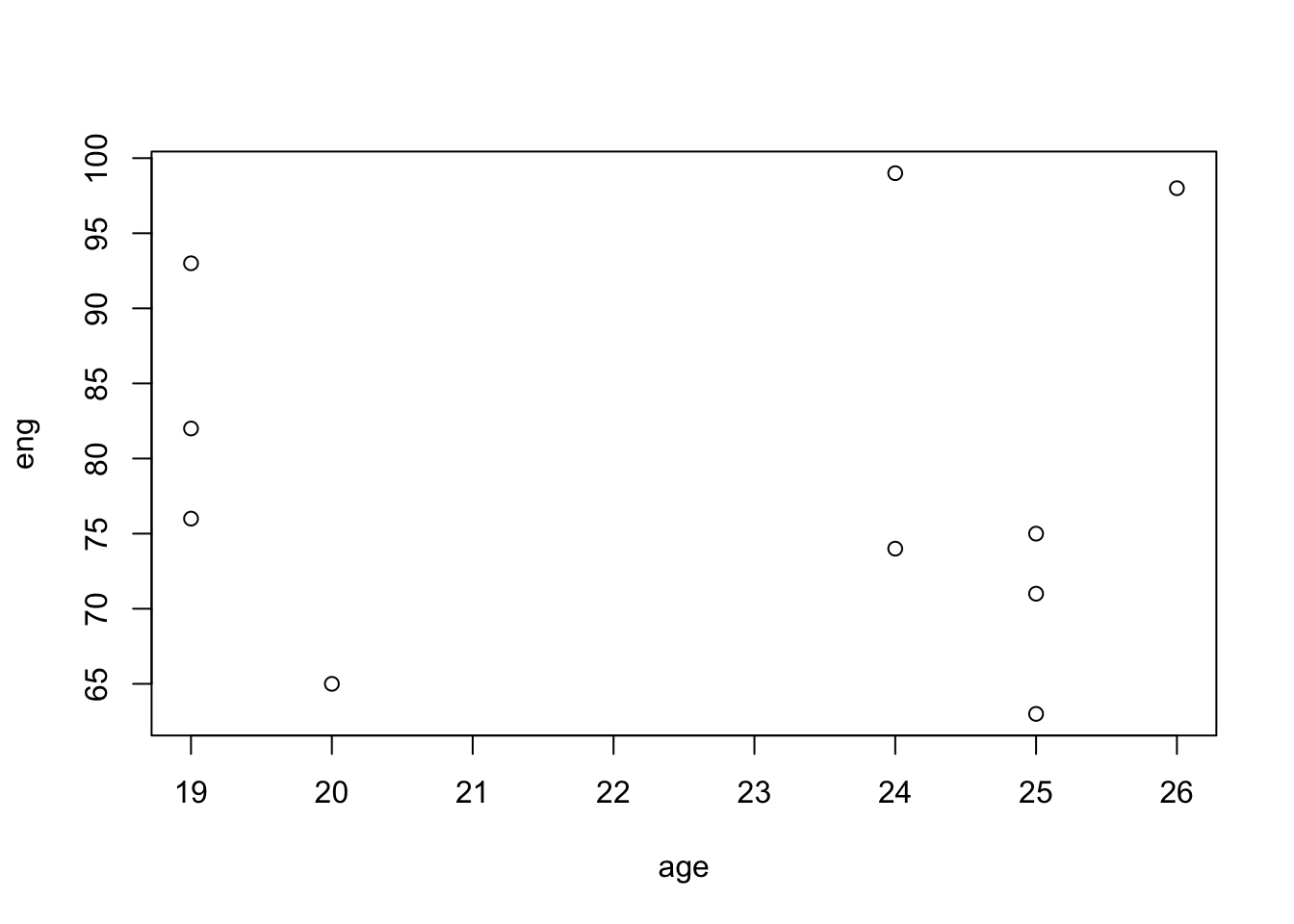
다음과 같이 성적을 데이터 프레임에 저장한 뒤 산점도를 그릴 수 있다.

ageeng <- data.frame(age = age, eng = eng)
plot(eng~age, data=ageeng)

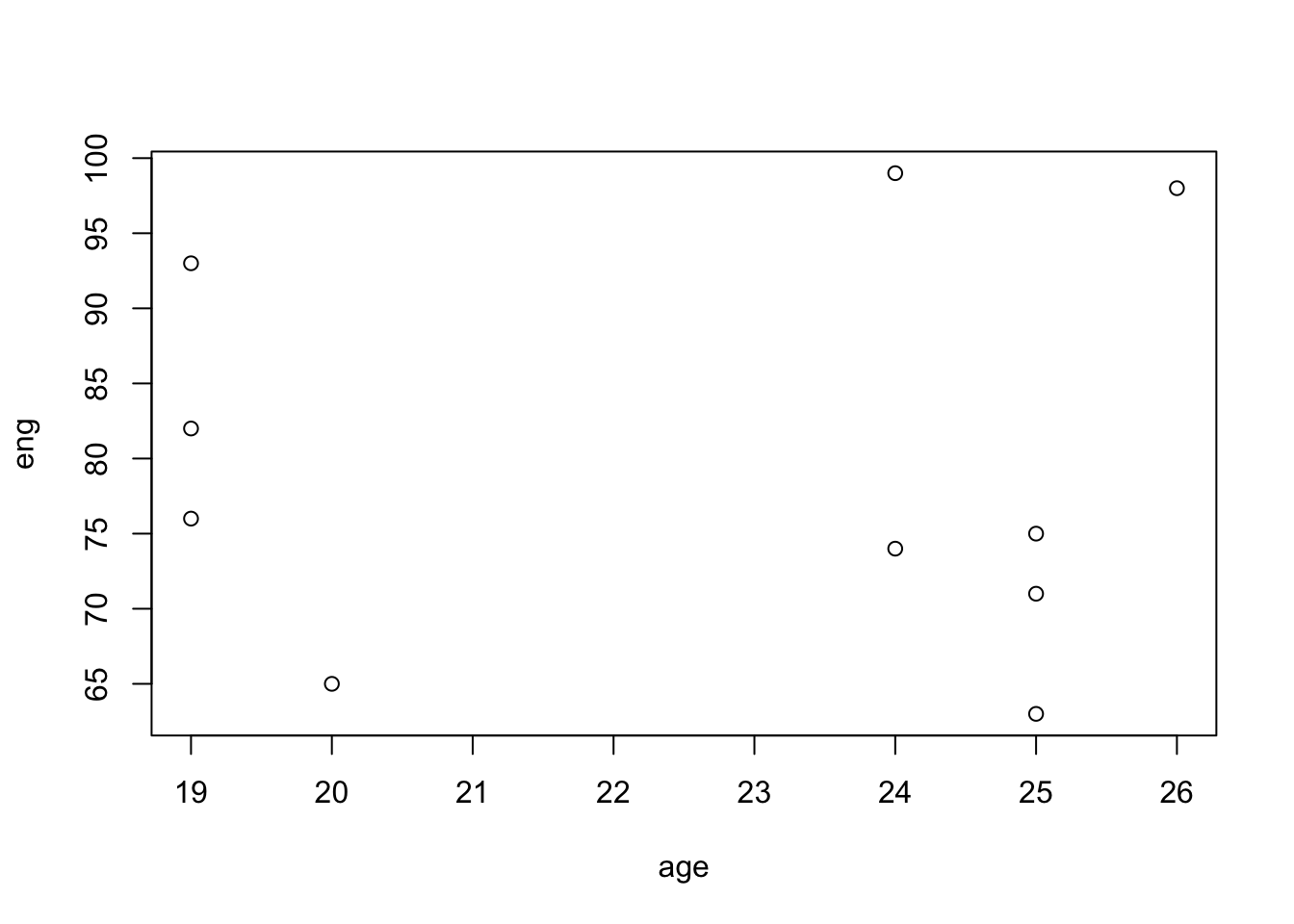
plot() 함수에도 다양한 매개변수가 있다.
대표적으로 다음과 같은 매개변수들이 있다.

매개변수	의미
x	x축 변수
y	y축 변수
main	그래프 제목
xlim	x축 좌표의 범위
ylim	y축 좌표의 범위
xlab	x축 제목
ylab	y축 제목
type	p : 관측치를 점으로 표현 (기본값) l : 관측치를 선으로 이어서 표현 c : 관측치를 점선으로 그려서 표현 n : 관측치를 나타내지 않음

par(family="NanumGothic") # only for mac user
plot(x=age,y=eng,main='나이와 영어 점수', xlab='나이', ylab='영어 점수')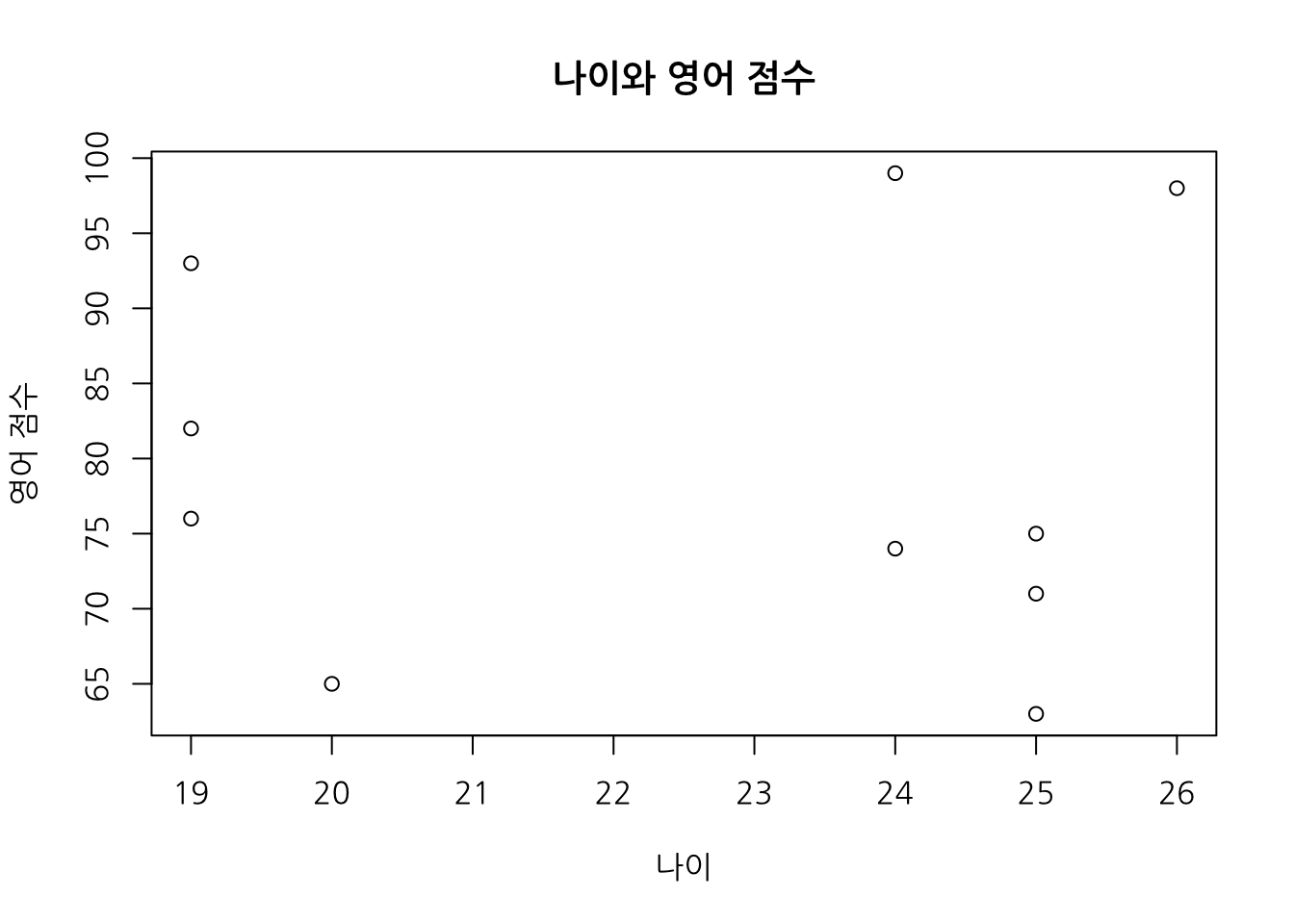

3.2 수치를 이용한 요약

3.2.1 상관계수

R에서 두 변수 사이의 (표본) 상관계수는 cor() 함수를 통해 계산할 수 있다.
위의 자료에서 나이와 영어 점수의 상관계수는 다음과 같이 계산할 수 있다.

cor(age,eng)

## [1] 0.01271089

실제 상관계수는 다음과 같이 계산할 수 있다.

\[ r_{xy} = \frac{cov(x,y)}{sd(x) sd(y)} \]

R을 이용해 계산해보면 같은 결과를 줌을 확인할 수 있다.
R에서 공분산을 계산하는 함수는 cov이다.

# with built-in functions
cov(age,eng)/(sd(age)*sd(eng))

## [1] 0.01271089

# directly
(sum(age*eng)-length(age)*mean(age)*mean(eng)) / 
  (sqrt(sum((age-mean(age))^2)*sum((eng-mean(eng))^2)))

## [1] 0.01271089

3.3 주의

수치를 이용한 요약은 해석에 주의해야 한다.


Datasaurus, source: Alberta Cairo
$N=142,r_{xy}=-0.0645$

4 예제

R에는 기본적으로 내장된 데이터들이 있다.
그 중 가장 유명한 것으로 아이리스(붓꽃)의 특성들을 기록한 iris 자료가 있다.
iris는 통계학자 Fisher가 소개한 데이터로, 붓꽃의 3가지 종 setosa, versicolor, virginica에 대해 꽃받침(sepal)과 꽃잎(petal)의 길이와 너비를 정리한 것이다.
구체적으로, iris 데이터의 성분은 다음으로 이루어져있다.

열	의미	자료형
Sepal.Length	꽃받침의 길이	숫자형
Sepal.Width	꽃받침의 너비	숫자형
Petal.Length	꽃잎의 길이	숫자형
Petal.Width	꽃잎의 너비	숫자형
Species	붓꽃의 종	범주형

R에서는 이미 iris 데이터가 저장되어 있기 때문에, 바로 데이터를 다룰 수 있다.

head(iris)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

여기서는 다음과 같이 iris.txt 자료를 직접 다운로드 받아 read.table() 함수를 이용해 불러와보자.
먼저 다음 링크를 클릭하여 iris.txt를 다운로드 받자.
주로 자료의 첫 번째 행은 변수명을 나타내는 경우가 많은데, 이처럼 첫 번째 행을 관측치가 아닌 변수명으로 인식하도록 하기 위해서는 header=T를 사용한다.
다음과 같이 iris.txt 파일을 R에 불러오고 iris_data에 저장하자.

iris_data <- read.table('iris.txt',header=T)
head(iris_data)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

이렇게 불러온 자료는 데이터 프레임의 형태로 저장되고 자료의 각 열(column)은 각각의 변수를 나타낸다.
데이터 프레임의 각 열을 사용하기 위해서는 $변수명을 사용한다.
예를 들어 iris 데이터의 첫 번째 열인 Sepal.Length 변수를 사용하기 위해서는 iris_data$Sepal.Length를 입력한다

iris_data$Sepal.Length

##   [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9 5.4 4.8 4.8 4.3 5.8 5.7 5.4
##  [18] 5.1 5.7 5.1 5.4 5.1 4.6 5.1 4.8 5.0 5.0 5.2 5.2 4.7 4.8 5.4 5.2 5.5
##  [35] 4.9 5.0 5.5 4.9 4.4 5.1 5.0 4.5 4.4 5.0 5.1 4.8 5.1 4.6 5.3 5.0 7.0
##  [52] 6.4 6.9 5.5 6.5 5.7 6.3 4.9 6.6 5.2 5.0 5.9 6.0 6.1 5.6 6.7 5.6 5.8
##  [69] 6.2 5.6 5.9 6.1 6.3 6.1 6.4 6.6 6.8 6.7 6.0 5.7 5.5 5.5 5.8 6.0 5.4
##  [86] 6.0 6.7 6.3 5.6 5.5 5.5 6.1 5.8 5.0 5.6 5.7 5.7 6.2 5.1 5.7 6.3 5.8
## [103] 7.1 6.3 6.5 7.6 4.9 7.3 6.7 7.2 6.5 6.4 6.8 5.7 5.8 6.4 6.5 7.7 7.7
## [120] 6.0 6.9 5.6 7.7 6.3 6.7 7.2 6.2 6.1 6.4 7.2 7.4 7.9 6.4 6.3 6.1 7.7
## [137] 6.3 6.4 6.0 6.9 6.7 6.9 5.8 6.8 6.7 6.7 6.3 6.5 6.2 5.9

Species 변수의 분할표를 다음과 같이 출력할 수 있다.

table(iris_data$Species)

## 
##     setosa versicolor  virginica 
##         50         50         50

각 종의 수가 균등하게 관측되어 있다는 것을 확인할 수 있다.
붓꽃의 꽃잎 길이의 평균은 다음과 같이 계산할 수 있다.

mean(iris_data$Petal.Length)

## [1] 3.758

이번에는 꽃잎의 길이와 꽃잎의 너비의 관계에 대해 알아보자.
다음과 같이 산점도를 그릴 수 있다.

plot(iris_data$Petal.Length,iris_data$Petal.Width,
     main='length and width of Petals',
     xlab='length', ylab='width')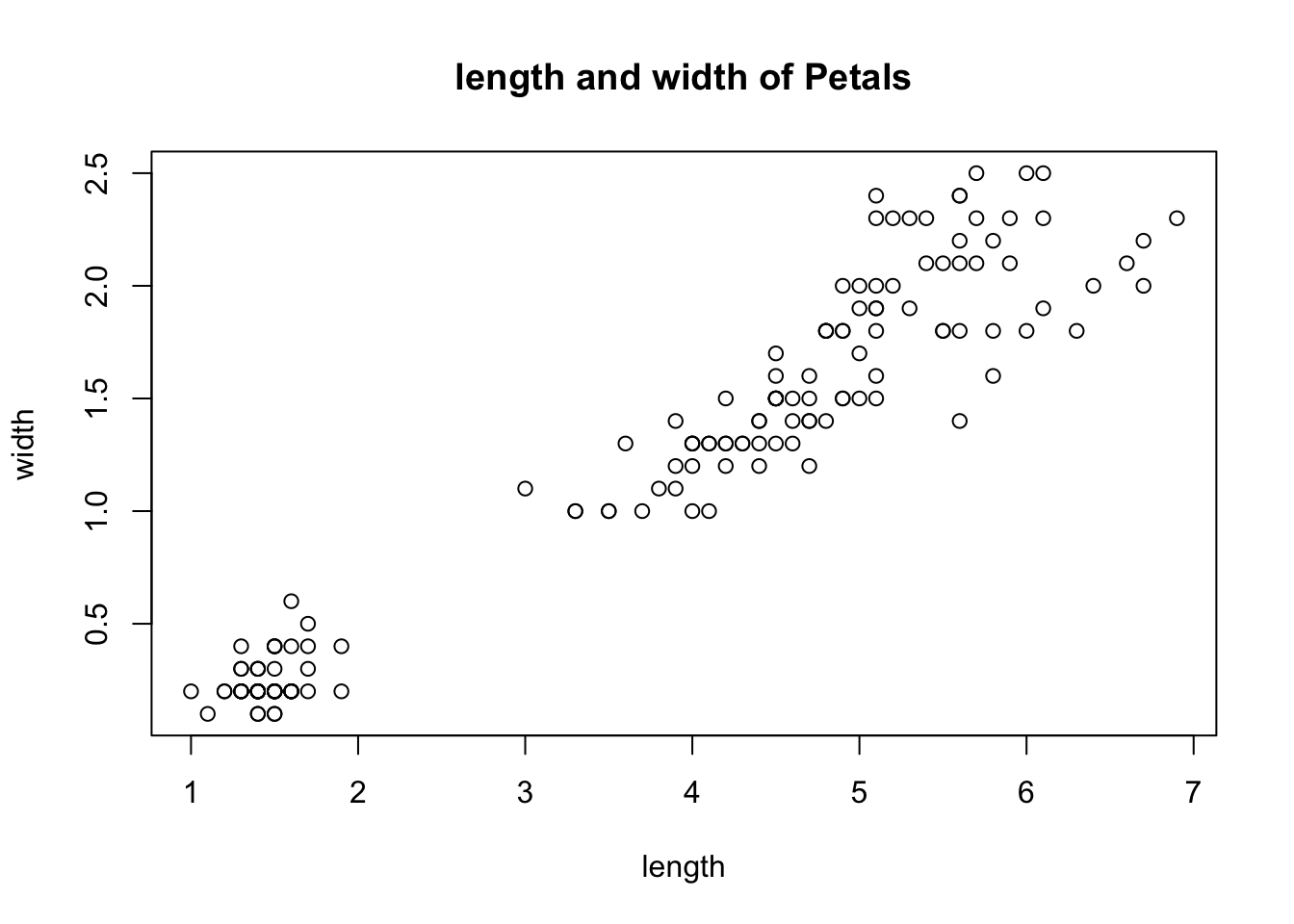

붓꽃의 꽃잎의 길이와 너비는 어느 정도 관계가 있는 것으로 보인다.
상관계수를 계산해보자.

cor(iris_data$Petal.Length,iris_data$Petal.Width)

## [1] 0.9628654

강한 양의 상관관계가 있다고 말할 수 있다.

과제

1번

BRFSS (The Behavioral Risk Factor Surveillance System)은 미국 CDC (Centers for Disease Control and Prevention)에서 매년 350,000명을 대상으로 실시하는 전화 설문조사이다.
이 자료는 2000년에 실시된 BRFSS 설문조사에서 임의추출된 20,000명에 대한 자료이며, 열 또한 전체 200여개 정도 중 9개 만을 선별한 것이다.
이 자료는 openintro.org에서 다운로드 받을 수 있으며, 보다 자세한 내용은 해당 홈페이지를 참고하면 된다.
자료의 열은 다음과 같은 성분들로 구성되어 있다.
- genhlth: A categorical vector indicating general health, with categories excellent, very good, good, fair, and poor.
- exerany: A categorical vector, 1 if the respondent exercised in the past month and 0 otherwise.
- hlthplan: A categorical vector, 1 if the respondent has some form of health coverage and 0 otherwise.
- smoke100: A categorical vector, 1 if the respondent has smoked at least 100 cigarettes in their entire life and 0 otherwise.
- height: A numerical vector, respondent’s height in inches.
- weight: A numerical vector, respondent’s weight in pounds.
- wtdesire: A numerical vector, respondent’s desired weight in pounds.
- age: A numerical vector, respondent’s age in years.
- gender: A categorical vector, respondent’s gender.
다음 링크에서 csv 파일을 다운로드 받은 뒤, 다음과 같이 자료를 불러오자.

cdc <- read.csv('cdc.csv')
head(cdc) # print head of the file.

##     genhlth exerany hlthplan smoke100 height weight wtdesire age gender
## 1      good       0        1        0     70    175      175  77      m
## 2      good       0        1        1     64    125      115  33      f
## 3      good       1        1        1     60    105      105  49      f
## 4      good       1        1        0     66    132      124  42      f
## 5 very good       0        1        0     61    150      130  55      f
## 6 very good       1        1        0     64    114      114  55      f

다음 물음들에 대하여 답하여라.

참고(20180921)

head() 함수는 data frame의 일부분을 출력하는 함수라는 것을 수업시간에 언급했습니다.
실제 과제는 전체 자료인 cdc를 이용해서 푸셔야 합니다.

1. (a)

genhlth⁴ 변수의 분할표를 작성하고, 이를 genhealth_table 변수에 저장하여라.

Solution

genhealth_table <- table(cdc$genhlth)

1. (b)

weight 변수의 히스토그램을 그려보아라.

Solution

hist(cdc$weight)

1. (c)

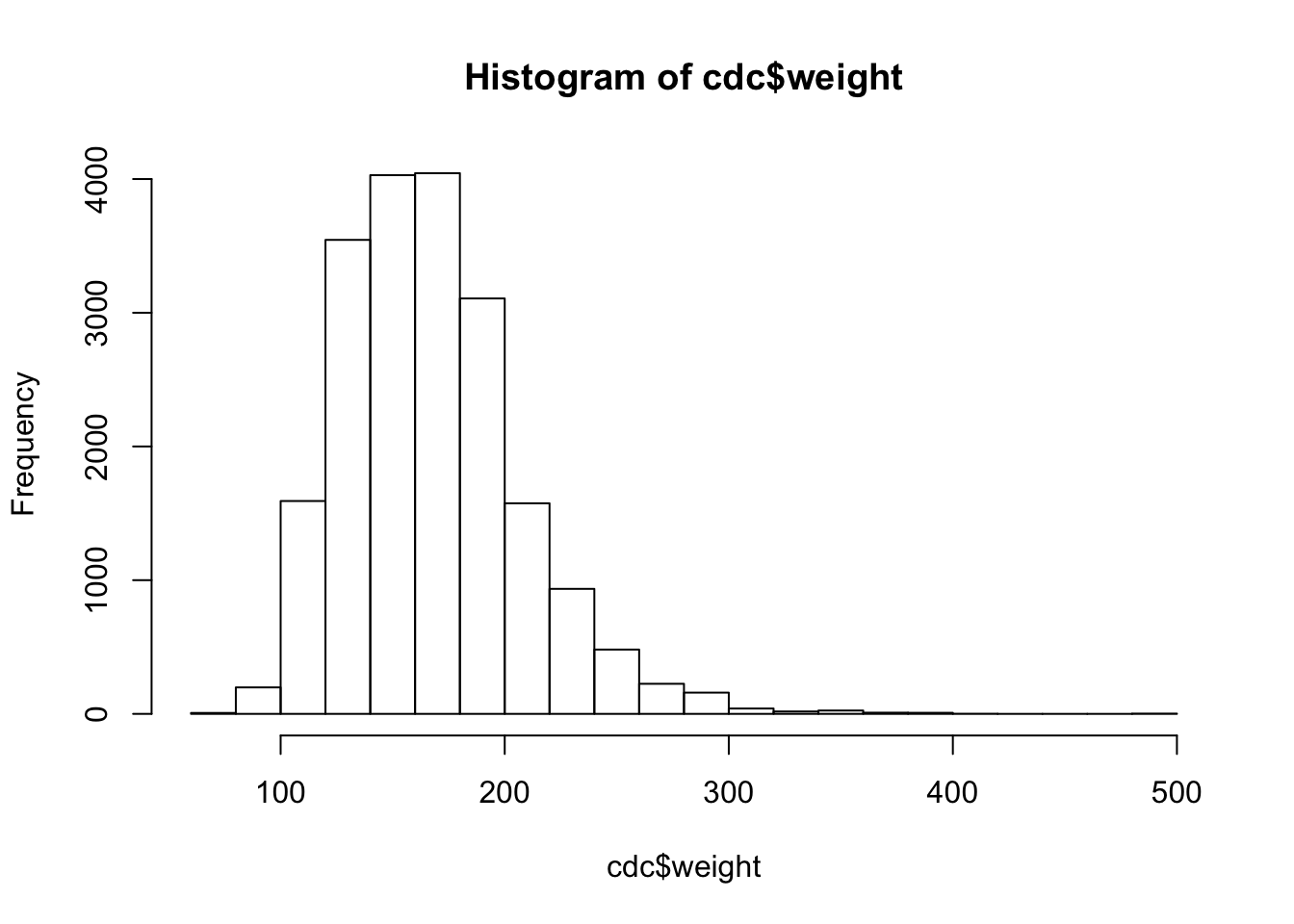
weight 변수의 5가지 요약 수치를 계산하고, 이를 weight_summary 변수에 저장하여라.

Solution

weight_summary <- fivenum(cdc$weight)

1. (d)

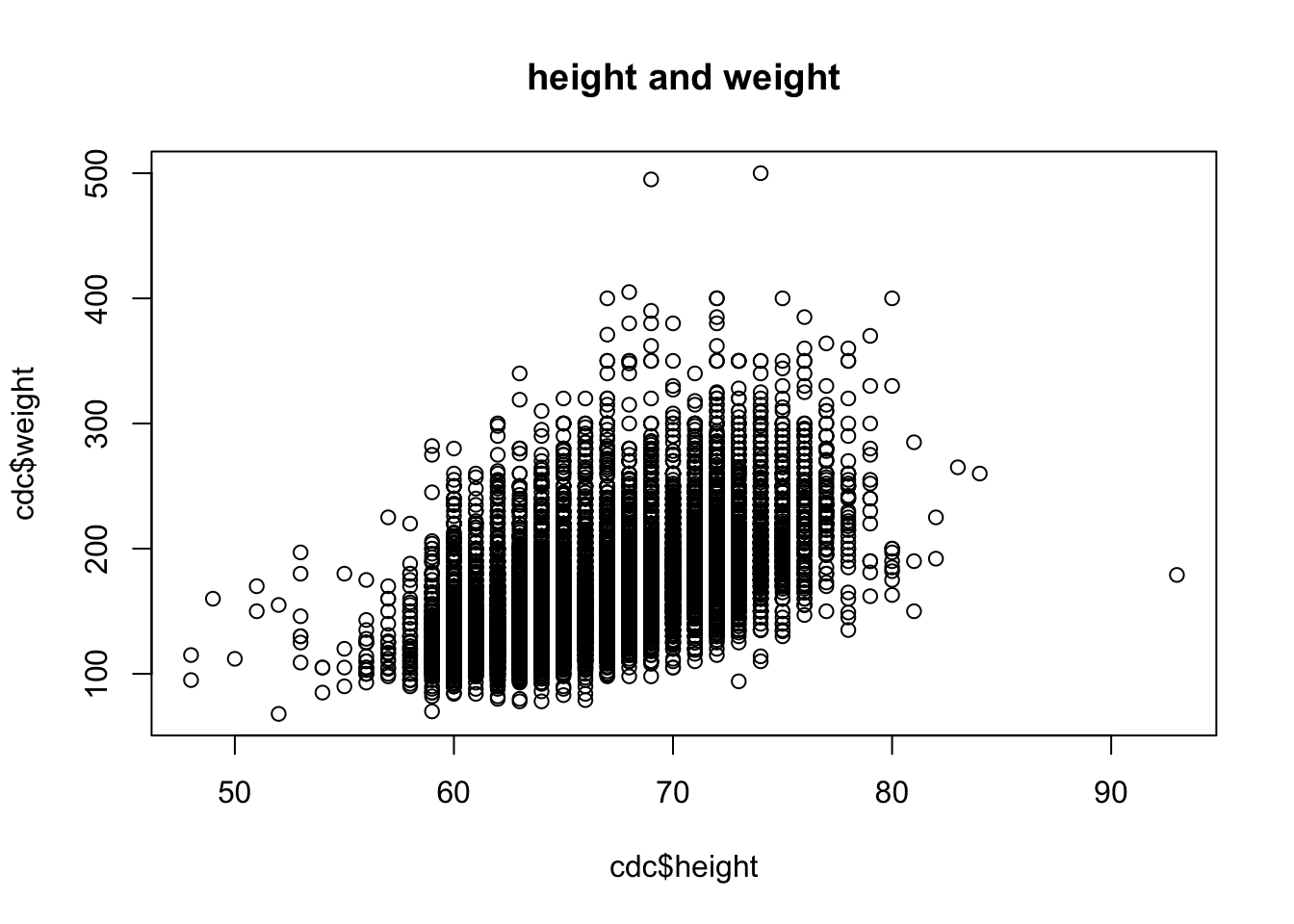
height 변수와 weight 변수의 산점도를 그려보아라. 이때, x축이 height, y축이 weight가 오게 하고, 산점도의 제목은 height and weight로 하여라.

Solution

plot(cdc$height, cdc$weight, main = "height and weight")

1. (e)

height 변수와 weight 변수의 상관계수를 계산하고, 이를 corr_hw 변수에 저장하여라.

Solution

corr_hw <- cor(cdc$height, cdc$weight)

2번 (조별과제)

이 문제는 조원들 중 한 명만 이메일로 제출하면 됩니다.
과제는 R 파일로 정리하여 조교 이메일로 보내주시면 됩니다.
eTL에 제출하실 필요는 없습니다.
메일 안에는 조와 조원 이름을 함께 명시하여 보내주시기 바랍니다.

2. (a)

조원들의 이름을 name 변수에 저장하여라.

2. (b)

조원들의 성별을 gender 변수에 저장하여라. (M or F)

2. (c)

조원들이 스스로 받을 것이라 생각하는 학점을 p_grade 변수에 저장하여라. (A+, A0 등)

2. (d)

조원들이 스스로 받기를 희망하는 학점을 w_grade 변수에 저장하여라. (A+, A0 등)

2. (e)

조원들의 학번을 숫자 형태로 number 변수에 저장하여라. (15, 18 등)

Wikipedia, 기술통계학, Link.↩
Wikipedia, 상자 수염 그림, Link.↩
Wikipedia, 5가지 요약 수치, Link.↩
기존에는 genhealth 으로 오타가 있었으나 9월 20일에 수정되었음.↩

기술 통계학

2018 가을학기 통계학실험 010 강좌

이경원

September 18, 2018

1 기술 통계학

2 일변량 자료의 요약

2.1 그래프를 이용한 요약

2.1.1 히스토그램

2.1.2 줄기-잎 그림

2.1.3 상자그림

2.2 수치를 이용한 요약

2.2.1 범주형 자료의 요약

2.2.2 숫자형 자료의 요약

3 이변량 자료의 요약

3.1 그래프를 이용한 요약

3.1.1 산점도

3.2 수치를 이용한 요약

3.2.1 상관계수

3.3 주의

4 예제

과제

1번

참고(20180921)

1. (a)

Solution

1. (b)

Solution

1. (c)

Solution

1. (d)

Solution

1. (e)

Solution

2번 (조별과제)

2. (a)

2. (b)

2. (c)

2. (d)

2. (e)

나이	성별	수학	영어
19	M	56	76
25	M	74	63
19	F	79	93
24	F	69	99
26	M	68	98
20	F	88	65
24	F	94	74
25	M	54	71
19	F	53	82
25	M	66	75

나이	성별	수학	영어
19	M	56	76
25	M	74	63
19	F	79	93
24	F	69	99
26	M	68	98
20	F	88	65
24	F	94	74
25	M	54	71
19	F	53	82
25	M	66	75

나이	성별	수학	영어
19	M	56	76
25	M	74	63
19	F	79	93
24	F	69	99
26	M	68	98
20	F	88	65
24	F	94	74
25	M	54	71
19	F	53	82
25	M	66	75